| Preprint | |
| Report number | arXiv:2208.03333 ; CERN-TH-2022-133 |
| Title | Overcoming exponential scaling with system size in Trotter-Suzuki implementations of constrained Hamiltonians: 2+1 U(1) lattice gauge theories |
| Author(s) | Grabowska, Dorota M. (CERN) ; Kane, Christopher (Arizona U.) ; Nachman, Benjamin (LBL, Berkeley) ; Bauer, Christian W. (LBL, Berkeley) |
| Imprint | 2022-08-05 |
| Number of pages | 9 |
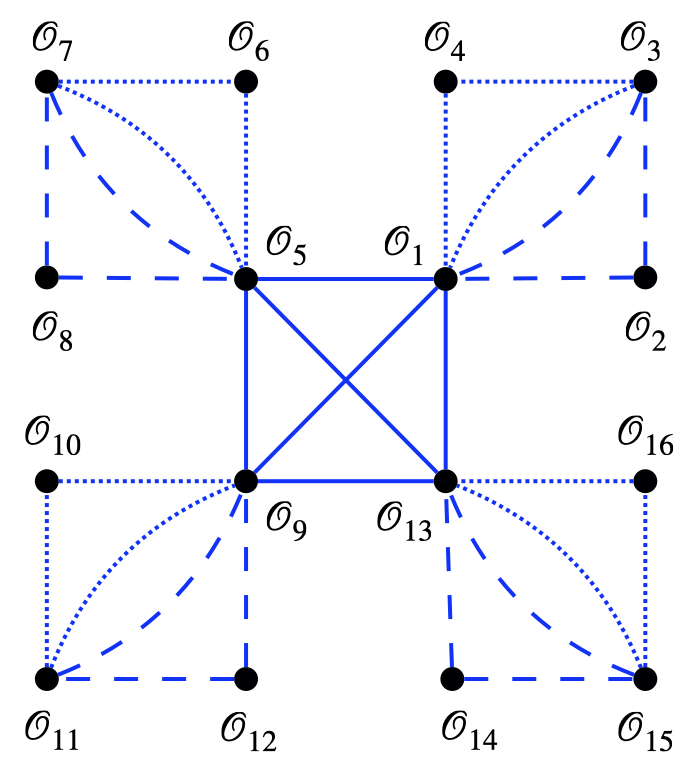
| Note | 9 pages, 1 Figure. V2 clarifies how to calculate the Degree of Coupling and how weaved matrices are constructed to reduce the Degree of Coupling |
| Subject category | hep-ph ; Particle Physics - Phenomenology ; hep-lat ; Particle Physics - Lattice ; quant-ph ; General Theoretical Physics |
| Abstract | For many quantum systems of interest, the classical computational cost of simulating their time evolution scales exponentially in the system size. At the same time, quantum computers have been shown to allow for simulations of some of these systems using resources that scale polynomially with the system size. Given the potential for using quantum computers for simulations that are not feasible using classical devices, it is paramount that one studies the scaling of quantum algorithms carefully. This work identifies a term in the Hamiltonian of a class of constrained systems that naively requires quantum resources that scale exponentially in the system size. An important example is a compact U(1) gauge theory on lattices with periodic boundary conditions. Imposing the magnetic Gauss' law a priori introduces a constraint into that Hamiltonian that naively results in an exponentially deep circuit. A method is then developed that reduces this scaling to polynomial in the system size, using a redefinition of the operator basis. An explicit construction of the matrices defining the change of operator basis, as well as the scaling of the associated computational cost, is given. |
| Other source | Inspire |
| Copyright/License | preprint: (License: CC BY 4.0) |
Notice créée le 2022-08-10, modifiée le 2023-01-31