Introduction aux tenseurs

Voir sur TensorFlow.org Exécuter dans Google Colab Voir la source sur GitHub Télécharger le cahier
import tensorflow as tf
import numpy as np

Les tenseurs sont des tableaux multidimensionnels avec un type uniforme (appelé dtype ). Vous pouvez voir tous les dtypes pris en charge sur tf.dtypes.DType .

Si vous êtes familier avec NumPy , les tenseurs sont (en quelque sorte) comme np.arrays .

Tous les tenseurs sont immuables comme les nombres et les chaînes Python : vous ne pouvez jamais mettre à jour le contenu d'un tenseur, mais seulement en créer un nouveau.

Bases

Créons quelques tenseurs de base.

Voici un tenseur "scalaire" ou "rang-0". Un scalaire contient une seule valeur et aucun "axe".

# This will be an int32 tensor by default; see "dtypes" below.
rank_0_tensor = tf.constant(4)
print(rank_0_tensor)

tf.Tensor(4, shape=(), dtype=int32)

Un tenseur "vecteur" ou "rang 1" est comme une liste de valeurs. Un vecteur a un axe :

# Let's make this a float tensor.
rank_1_tensor = tf.constant([2.0, 3.0, 4.0])
print(rank_1_tensor)

tf.Tensor([2. 3. 4.], shape=(3,), dtype=float32)

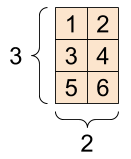
Un tenseur "matrice" ou "rang 2" a deux axes :

# If you want to be specific, you can set the dtype (see below) at creation time
rank_2_tensor = tf.constant([[1, 2],
                             [3, 4],
                             [5, 6]], dtype=tf.float16)
print(rank_2_tensor)

tf.Tensor(
[[1. 2.]
 [3. 4.]
 [5. 6.]], shape=(3, 2), dtype=float16)
Un scalaire, forme : [] Un vecteur, forme : [3] Une matrice, forme : [3, 2]
Un scalaire, le nombre 4La ligne avec 3 sections, chacune contenant un numéro.Une grille 3x2, chaque cellule contenant un nombre.

Les tenseurs peuvent avoir plus d'axes ; voici un tenseur à trois axes :

# There can be an arbitrary number of
# axes (sometimes called "dimensions")
rank_3_tensor = tf.constant([
  [[0, 1, 2, 3, 4],
   [5, 6, 7, 8, 9]],
  [[10, 11, 12, 13, 14],
   [15, 16, 17, 18, 19]],
  [[20, 21, 22, 23, 24],
   [25, 26, 27, 28, 29]],])

print(rank_3_tensor)

tf.Tensor(
[[[ 0  1  2  3  4]
  [ 5  6  7  8  9]]

 [[10 11 12 13 14]
  [15 16 17 18 19]]

 [[20 21 22 23 24]
  [25 26 27 28 29]]], shape=(3, 2, 5), dtype=int32)

Il existe de nombreuses façons de visualiser un tenseur avec plus de deux axes.

Un tenseur 3 axes, forme : [3, 2, 5]

Vous pouvez convertir un tenseur en un tableau NumPy en utilisant np.array ou la méthode tensor.numpy :

np.array(rank_2_tensor)

array([[1., 2.],
       [3., 4.],
       [5., 6.]], dtype=float16)

rank_2_tensor.numpy()

array([[1., 2.],
       [3., 4.],
       [5., 6.]], dtype=float16)

Les tenseurs contiennent souvent des flottants et des entiers, mais ont de nombreux autres types, notamment :

  • nombres complexes
  • cordes

La classe de base tf.Tensor exige que les tenseurs soient "rectangulaires" --- c'est-à-dire que le long de chaque axe, chaque élément ait la même taille. Cependant, il existe des types spécialisés de tenseurs qui peuvent gérer différentes formes :

Vous pouvez faire des calculs de base sur les tenseurs, y compris l'addition, la multiplication élément par élément et la multiplication matricielle.

a = tf.constant([[1, 2],
                 [3, 4]])
b = tf.constant([[1, 1],
                 [1, 1]]) # Could have also said `tf.ones([2,2])`

print(tf.add(a, b), "\n")
print(tf.multiply(a, b), "\n")
print(tf.matmul(a, b), "\n")

tf.Tensor(
[[2 3]
 [4 5]], shape=(2, 2), dtype=int32) 

tf.Tensor(
[[1 2]
 [3 4]], shape=(2, 2), dtype=int32) 

tf.Tensor(
[[3 3]
 [7 7]], shape=(2, 2), dtype=int32)

print(a + b, "\n") # element-wise addition
print(a * b, "\n") # element-wise multiplication
print(a @ b, "\n") # matrix multiplication

tf.Tensor(
[[2 3]
 [4 5]], shape=(2, 2), dtype=int32) 

tf.Tensor(
[[1 2]
 [3 4]], shape=(2, 2), dtype=int32) 

tf.Tensor(
[[3 3]
 [7 7]], shape=(2, 2), dtype=int32)

Les tenseurs sont utilisés dans toutes sortes d'opérations (ops).

c = tf.constant([[4.0, 5.0], [10.0, 1.0]])

# Find the largest value
print(tf.reduce_max(c))
# Find the index of the largest value
print(tf.argmax(c))
# Compute the softmax
print(tf.nn.softmax(c))

tf.Tensor(10.0, shape=(), dtype=float32)
tf.Tensor([1 0], shape=(2,), dtype=int64)
tf.Tensor(
[[2.6894143e-01 7.3105854e-01]
 [9.9987662e-01 1.2339458e-04]], shape=(2, 2), dtype=float32)

À propos des formes

Les tenseurs ont des formes. Un peu de vocabulaire :

  • Forme : La longueur (nombre d'éléments) de chacun des axes d'un tenseur.
  • Rang : Nombre d'axes tenseurs. Un scalaire est de rang 0, un vecteur de rang 1, une matrice de rang 2.
  • Axe ou Dimension : Une dimension particulière d'un tenseur.
  • Taille : Le nombre total d'éléments dans le tenseur, le vecteur de forme du produit.

Les objets Tensors et tf.TensorShape ont des propriétés pratiques pour y accéder :

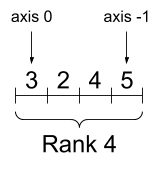
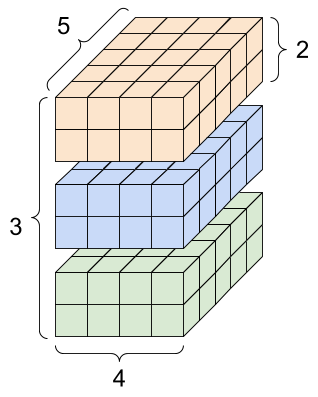
rank_4_tensor = tf.zeros([3, 2, 4, 5])
Un tenseur de rang 4, forme : [3, 2, 4, 5]
Une forme de tenseur est comme un vecteur.Un tenseur 4 axes
print("Type of every element:", rank_4_tensor.dtype)
print("Number of axes:", rank_4_tensor.ndim)
print("Shape of tensor:", rank_4_tensor.shape)
print("Elements along axis 0 of tensor:", rank_4_tensor.shape[0])
print("Elements along the last axis of tensor:", rank_4_tensor.shape[-1])
print("Total number of elements (3*2*4*5): ", tf.size(rank_4_tensor).numpy())

Type of every element: <dtype: 'float32'>
Number of axes: 4
Shape of tensor: (3, 2, 4, 5)
Elements along axis 0 of tensor: 3
Elements along the last axis of tensor: 5
Total number of elements (3*2*4*5):  120

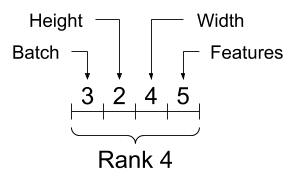
Bien que les axes soient souvent désignés par leurs indices, vous devez toujours garder une trace de la signification de chacun. Souvent, les axes sont classés du global au local : l'axe du lot en premier, suivi des dimensions spatiales et des caractéristiques de chaque emplacement en dernier. De cette façon, les vecteurs de caractéristiques sont des régions contiguës de la mémoire.

Ordre typique des axes
Gardez une trace de ce que chaque axe est. Un tenseur à 4 axes peut être : Lot, Largeur, Hauteur, Caractéristiques

Indexage

Indexation mono-axe

TensorFlow suit les règles d'indexation Python standard, similaires à l'indexation d'une liste ou d'une chaîne dans Python , et les règles de base de l'indexation NumPy.

  • les index commencent à 0
  • les indices négatifs comptent à rebours à partir de la fin
  • les deux-points, : , sont utilisés pour les tranches : start:stop:step
rank_1_tensor = tf.constant([0, 1, 1, 2, 3, 5, 8, 13, 21, 34])
print(rank_1_tensor.numpy())

[ 0  1  1  2  3  5  8 13 21 34]

L'indexation avec un scalaire supprime l'axe :

print("First:", rank_1_tensor[0].numpy())
print("Second:", rank_1_tensor[1].numpy())
print("Last:", rank_1_tensor[-1].numpy())

First: 0
Second: 1
Last: 34

L'indexation avec une tranche : conserve l'axe :

print("Everything:", rank_1_tensor[:].numpy())
print("Before 4:", rank_1_tensor[:4].numpy())
print("From 4 to the end:", rank_1_tensor[4:].numpy())
print("From 2, before 7:", rank_1_tensor[2:7].numpy())
print("Every other item:", rank_1_tensor[::2].numpy())
print("Reversed:", rank_1_tensor[::-1].numpy())

Everything: [ 0  1  1  2  3  5  8 13 21 34]
Before 4: [0 1 1 2]
From 4 to the end: [ 3  5  8 13 21 34]
From 2, before 7: [1 2 3 5 8]
Every other item: [ 0  1  3  8 21]
Reversed: [34 21 13  8  5  3  2  1  1  0]

Indexation multi-axes

Les tenseurs de rang supérieur sont indexés en passant plusieurs indices.

Les mêmes règles que dans le cas d'un seul axe s'appliquent à chaque axe indépendamment.

print(rank_2_tensor.numpy())

[[1. 2.]
 [3. 4.]
 [5. 6.]]

En passant un entier pour chaque index, le résultat est un scalaire.

# Pull out a single value from a 2-rank tensor
print(rank_2_tensor[1, 1].numpy())

4.0

Vous pouvez indexer à l'aide de n'importe quelle combinaison d'entiers et de tranches :

# Get row and column tensors
print("Second row:", rank_2_tensor[1, :].numpy())
print("Second column:", rank_2_tensor[:, 1].numpy())
print("Last row:", rank_2_tensor[-1, :].numpy())
print("First item in last column:", rank_2_tensor[0, -1].numpy())
print("Skip the first row:")
print(rank_2_tensor[1:, :].numpy(), "\n")

Second row: [3. 4.]
Second column: [2. 4. 6.]
Last row: [5. 6.]
First item in last column: 2.0
Skip the first row:
[[3. 4.]
 [5. 6.]]

Voici un exemple avec un tenseur 3 axes :

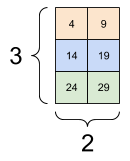
print(rank_3_tensor[:, :, 4])

tf.Tensor(
[[ 4  9]
 [14 19]
 [24 29]], shape=(3, 2), dtype=int32)
Sélection de la dernière entité dans tous les emplacements de chaque exemple du lot
Un tenseur 3x2x5 avec toutes les valeurs à l'index-4 du dernier axe sélectionné.Les valeurs sélectionnées sont regroupées dans un tenseur à 2 axes.

Lisez le guide de découpage des tenseurs pour savoir comment vous pouvez appliquer l'indexation pour manipuler des éléments individuels dans vos tenseurs.

Manipuler des formes

Remodeler un tenseur est d'une grande utilité.

# Shape returns a `TensorShape` object that shows the size along each axis
x = tf.constant([[1], [2], [3]])
print(x.shape)

(3, 1)

# You can convert this object into a Python list, too
print(x.shape.as_list())

[3, 1]

Vous pouvez remodeler un tenseur en une nouvelle forme. L'opération tf.reshape est rapide et peu coûteuse car les données sous-jacentes n'ont pas besoin d'être dupliquées.

# You can reshape a tensor to a new shape.
# Note that you're passing in a list
reshaped = tf.reshape(x, [1, 3])

print(x.shape)
print(reshaped.shape)

(3, 1)
(1, 3)

Les données conservent leur disposition en mémoire et un nouveau tenseur est créé, avec la forme demandée, pointant vers les mêmes données. TensorFlow utilise l'ordre de mémoire "row-major" de style C, où l'incrémentation de l'index le plus à droite correspond à une seule étape en mémoire.

print(rank_3_tensor)

tf.Tensor(
[[[ 0  1  2  3  4]
  [ 5  6  7  8  9]]

 [[10 11 12 13 14]
  [15 16 17 18 19]]

 [[20 21 22 23 24]
  [25 26 27 28 29]]], shape=(3, 2, 5), dtype=int32)

Si vous aplatissez un tenseur, vous pouvez voir dans quel ordre il est disposé en mémoire.

# A `-1` passed in the `shape` argument says "Whatever fits".
print(tf.reshape(rank_3_tensor, [-1]))

tf.Tensor(
[ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
 24 25 26 27 28 29], shape=(30,), dtype=int32)

Généralement, la seule utilisation raisonnable de tf.reshape est de combiner ou de diviser des axes adjacents (ou d'ajouter/supprimer 1 s).

Pour ce tenseur 3x2x5, le remodelage en (3x2)x5 ou 3x(2x5) sont deux choses raisonnables à faire, car les tranches ne se mélangent pas :

print(tf.reshape(rank_3_tensor, [3*2, 5]), "\n")
print(tf.reshape(rank_3_tensor, [3, -1]))

tf.Tensor(
[[ 0  1  2  3  4]
 [ 5  6  7  8  9]
 [10 11 12 13 14]
 [15 16 17 18 19]
 [20 21 22 23 24]
 [25 26 27 28 29]], shape=(6, 5), dtype=int32) 

tf.Tensor(
[[ 0  1  2  3  4  5  6  7  8  9]
 [10 11 12 13 14 15 16 17 18 19]
 [20 21 22 23 24 25 26 27 28 29]], shape=(3, 10), dtype=int32)
Quelques bons remodelages.
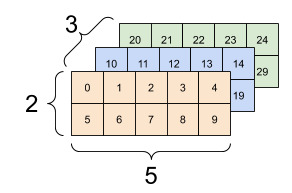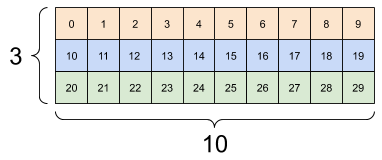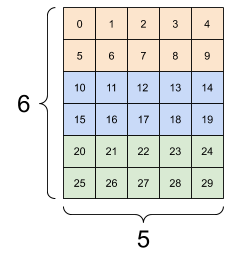Un tenseur 3x2x5Les mêmes données reformées en (3x2)x5Les mêmes données reformées en 3x(2x5)

Le remodelage "fonctionnera" pour toute nouvelle forme avec le même nombre total d'éléments, mais il ne fera rien d'utile si vous ne respectez pas l'ordre des axes.

L'échange d'axes dans tf.reshape ne fonctionne pas ; vous avez besoin de tf.transpose pour cela.

# Bad examples: don't do this

# You can't reorder axes with reshape.
print(tf.reshape(rank_3_tensor, [2, 3, 5]), "\n") 

# This is a mess
print(tf.reshape(rank_3_tensor, [5, 6]), "\n")

# This doesn't work at all
try:
  tf.reshape(rank_3_tensor, [7, -1])
except Exception as e:
  print(f"{type(e).__name__}: {e}")

tf.Tensor(
[[[ 0  1  2  3  4]
  [ 5  6  7  8  9]
  [10 11 12 13 14]]

 [[15 16 17 18 19]
  [20 21 22 23 24]
  [25 26 27 28 29]]], shape=(2, 3, 5), dtype=int32) 

tf.Tensor(
[[ 0  1  2  3  4  5]
 [ 6  7  8  9 10 11]
 [12 13 14 15 16 17]
 [18 19 20 21 22 23]
 [24 25 26 27 28 29]], shape=(5, 6), dtype=int32) 

InvalidArgumentError: Input to reshape is a tensor with 30 values, but the requested shape requires a multiple of 7 [Op:Reshape]
Quelques mauvais remodelages.
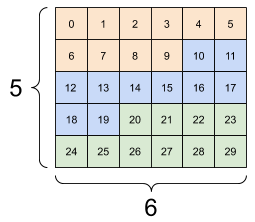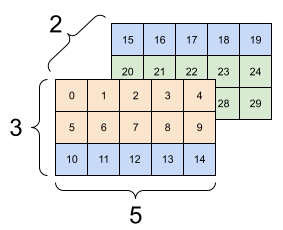Vous ne pouvez pas réorganiser les axes, utilisez tf.transpose pour celaTout ce qui mélange les tranches de données est probablement faux.La nouvelle forme doit correspondre exactement.

Vous pouvez rencontrer des formes non entièrement spécifiées. Soit la forme contient un None (une longueur d'axe est inconnue), soit la forme entière est None (le rang du tenseur est inconnu).

À l'exception de tf.RaggedTensor , ces formes ne se produiront que dans le contexte des API symboliques de création de graphes de TensorFlow :

En savoir plus sur les DTypes

Pour inspecter le type de données d'un tf.Tensor , utilisez la propriété Tensor.dtype .

Lors de la création d'un tf.Tensor à partir d'un objet Python, vous pouvez éventuellement spécifier le type de données.

Si vous ne le faites pas, TensorFlow choisit un type de données qui peut représenter vos données. TensorFlow convertit les entiers Python en tf.int32 et les nombres à virgule flottante Python en tf.float32 . Sinon, TensorFlow utilise les mêmes règles que NumPy lors de la conversion en tableaux.

Vous pouvez diffuser d'un type à l'autre.

the_f64_tensor = tf.constant([2.2, 3.3, 4.4], dtype=tf.float64)
the_f16_tensor = tf.cast(the_f64_tensor, dtype=tf.float16)
# Now, cast to an uint8 and lose the decimal precision
the_u8_tensor = tf.cast(the_f16_tensor, dtype=tf.uint8)
print(the_u8_tensor)

tf.Tensor([2 3 4], shape=(3,), dtype=uint8)

Diffusion

La diffusion est un concept emprunté à la fonctionnalité équivalente dans NumPy . En bref, sous certaines conditions, les tenseurs plus petits sont "étirés" automatiquement pour s'adapter aux tenseurs plus grands lors de l'exécution d'opérations combinées sur eux.

Le cas le plus simple et le plus courant est lorsque vous essayez de multiplier ou d'ajouter un tenseur à un scalaire. Dans ce cas, le scalaire est diffusé pour avoir la même forme que l'autre argument.

x = tf.constant([1, 2, 3])

y = tf.constant(2)
z = tf.constant([2, 2, 2])
# All of these are the same computation
print(tf.multiply(x, 2))
print(x * y)
print(x * z)

tf.Tensor([2 4 6], shape=(3,), dtype=int32)
tf.Tensor([2 4 6], shape=(3,), dtype=int32)
tf.Tensor([2 4 6], shape=(3,), dtype=int32)

De même, les axes de longueur 1 peuvent être étirés pour correspondre aux autres arguments. Les deux arguments peuvent être étirés dans le même calcul.

Dans ce cas, une matrice 3x1 est multipliée élément par élément par une matrice 1x4 pour produire une matrice 3x4. Notez que le premier 1 est facultatif : la forme de y est [4] .

# These are the same computations
x = tf.reshape(x,[3,1])
y = tf.range(1, 5)
print(x, "\n")
print(y, "\n")
print(tf.multiply(x, y))

tf.Tensor(
[[1]
 [2]
 [3]], shape=(3, 1), dtype=int32) 

tf.Tensor([1 2 3 4], shape=(4,), dtype=int32) 

tf.Tensor(
[[ 1  2  3  4]
 [ 2  4  6  8]
 [ 3  6  9 12]], shape=(3, 4), dtype=int32)
Une annonce diffusée : un [3, 1] fois un [1, 4] donne un [3,4]
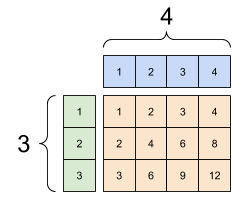L'ajout d'une matrice 3x1 à une matrice 4x1 donne une matrice 3x4

Voici la même opération sans diffusion :

x_stretch = tf.constant([[1, 1, 1, 1],
                         [2, 2, 2, 2],
                         [3, 3, 3, 3]])

y_stretch = tf.constant([[1, 2, 3, 4],
                         [1, 2, 3, 4],
                         [1, 2, 3, 4]])

print(x_stretch * y_stretch)  # Again, operator overloading

tf.Tensor(
[[ 1  2  3  4]
 [ 2  4  6  8]
 [ 3  6  9 12]], shape=(3, 4), dtype=int32)

La plupart du temps, la diffusion est à la fois efficace en temps et en espace, car l'opération de diffusion ne matérialise jamais les tenseurs étendus en mémoire.

Vous voyez à quoi ressemble la diffusion en utilisant tf.broadcast_to .

print(tf.broadcast_to(tf.constant([1, 2, 3]), [3, 3]))

tf.Tensor(
[[1 2 3]
 [1 2 3]
 [1 2 3]], shape=(3, 3), dtype=int32)

Contrairement à une opération mathématique, par exemple, broadcast_to ne fait rien de spécial pour économiser de la mémoire. Ici, vous matérialisez le tenseur.

Cela peut devenir encore plus compliqué. Cette section du livre Python Data Science Handbook de Jake VanderPlas montre plus d'astuces de diffusion (encore une fois dans NumPy).

tf.convert_to_tensor

La plupart des opérations, comme tf.matmul et tf.reshape prennent des arguments de classe tf.Tensor . Cependant, vous remarquerez que dans le cas ci-dessus, les objets Python en forme de tenseurs sont acceptés.

La plupart des opérations, mais pas toutes, appellent convert_to_tensor sur des arguments non tenseurs. Il existe un registre des conversions et la plupart des classes d'objets telles que ndarray , TensorShape , Python lists et tf.Variable de NumPy seront toutes converties automatiquement.

Voir tf.register_tensor_conversion_function pour plus de détails, et si vous avez votre propre type, vous souhaitez convertir automatiquement en tenseur.

Tenseurs en lambeaux

Un tenseur avec un nombre variable d'éléments le long d'un axe est appelé "ragged". Utilisez tf.ragged.RaggedTensor pour les données irrégulières.

Par exemple, This ne peut pas être représenté comme un tenseur régulier :

A tf.RaggedTensor , forme : [4, None]
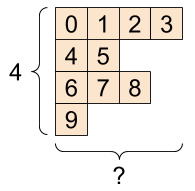Un tenseur irrégulier à 2 axes, chaque ligne peut avoir une longueur différente.
ragged_list = [
    [0, 1, 2, 3],
    [4, 5],
    [6, 7, 8],
    [9]]

try:
  tensor = tf.constant(ragged_list)
except Exception as e:
  print(f"{type(e).__name__}: {e}")

ValueError: Can't convert non-rectangular Python sequence to Tensor.

Créez plutôt un tf.RaggedTensor en utilisant tf.ragged.constant :

ragged_tensor = tf.ragged.constant(ragged_list)
print(ragged_tensor)

<tf.RaggedTensor [[0, 1, 2, 3], [4, 5], [6, 7, 8], [9]]>

La forme d'un tf.RaggedTensor contiendra des axes de longueurs inconnues :

print(ragged_tensor.shape)

(4, None)

Tenseurs de cordes

tf.string est un dtype , c'est-à-dire que vous pouvez représenter des données sous forme de chaînes (tableaux d'octets de longueur variable) dans des tenseurs.

Les chaînes sont atomiques et ne peuvent pas être indexées comme le sont les chaînes Python. La longueur de la corde n'est pas l'un des axes du tenseur. Voir tf.strings pour les fonctions permettant de les manipuler.

Voici un tenseur de chaîne scalaire :

# Tensors can be strings, too here is a scalar string.
scalar_string_tensor = tf.constant("Gray wolf")
print(scalar_string_tensor)

tf.Tensor(b'Gray wolf', shape=(), dtype=string)

Et un vecteur de chaînes :

Un vecteur de chaînes, forme : [3,]
La longueur de la chaîne n'est pas l'un des axes du tenseur.
# If you have three string tensors of different lengths, this is OK.
tensor_of_strings = tf.constant(["Gray wolf",
                                 "Quick brown fox",
                                 "Lazy dog"])
# Note that the shape is (3,). The string length is not included.
print(tensor_of_strings)

tf.Tensor([b'Gray wolf' b'Quick brown fox' b'Lazy dog'], shape=(3,), dtype=string)

Dans l'impression ci-dessus, le préfixe b indique que tf.string dtype n'est pas une chaîne unicode, mais une chaîne d'octets. Consultez le didacticiel Unicode pour en savoir plus sur l'utilisation du texte Unicode dans TensorFlow.

Si vous passez des caractères unicode, ils sont encodés en utf-8.

tf.constant("🥳👍")

<tf.Tensor: shape=(), dtype=string, numpy=b'\xf0\x9f\xa5\xb3\xf0\x9f\x91\x8d'>

Certaines fonctions de base avec des chaînes peuvent être trouvées dans tf.strings , y compris tf.strings.split .

# You can use split to split a string into a set of tensors
print(tf.strings.split(scalar_string_tensor, sep=" "))

tf.Tensor([b'Gray' b'wolf'], shape=(2,), dtype=string)

# ...but it turns into a `RaggedTensor` if you split up a tensor of strings,
# as each string might be split into a different number of parts.
print(tf.strings.split(tensor_of_strings))

<tf.RaggedTensor [[b'Gray', b'wolf'], [b'Quick', b'brown', b'fox'], [b'Lazy', b'dog']]>
Trois cordes séparées, forme : [3, None]
Le fractionnement de plusieurs chaînes renvoie un tf.RaggedTensor

Et tf.string.to_number :

text = tf.constant("1 10 100")
print(tf.strings.to_number(tf.strings.split(text, " ")))

tf.Tensor([  1.  10. 100.], shape=(3,), dtype=float32)

Bien que vous ne puissiez pas utiliser tf.cast pour transformer un tenseur de chaîne en nombres, vous pouvez le convertir en octets, puis en nombres.

byte_strings = tf.strings.bytes_split(tf.constant("Duck"))
byte_ints = tf.io.decode_raw(tf.constant("Duck"), tf.uint8)
print("Byte strings:", byte_strings)
print("Bytes:", byte_ints)

Byte strings: tf.Tensor([b'D' b'u' b'c' b'k'], shape=(4,), dtype=string)
Bytes: tf.Tensor([ 68 117  99 107], shape=(4,), dtype=uint8)

# Or split it up as unicode and then decode it
unicode_bytes = tf.constant("アヒル 🦆")
unicode_char_bytes = tf.strings.unicode_split(unicode_bytes, "UTF-8")
unicode_values = tf.strings.unicode_decode(unicode_bytes, "UTF-8")

print("\nUnicode bytes:", unicode_bytes)
print("\nUnicode chars:", unicode_char_bytes)
print("\nUnicode values:", unicode_values)

Unicode bytes: tf.Tensor(b'\xe3\x82\xa2\xe3\x83\x92\xe3\x83\xab \xf0\x9f\xa6\x86', shape=(), dtype=string)

Unicode chars: tf.Tensor([b'\xe3\x82\xa2' b'\xe3\x83\x92' b'\xe3\x83\xab' b' ' b'\xf0\x9f\xa6\x86'], shape=(5,), dtype=string)

Unicode values: tf.Tensor([ 12450  12498  12523     32 129414], shape=(5,), dtype=int32)

Le tf.string tf.string est utilisé pour toutes les données d'octets bruts dans TensorFlow. Le module tf.io contient des fonctions de conversion de données vers et à partir d'octets, y compris le décodage d'images et l'analyse csv.

Tenseurs clairsemés

Parfois, vos données sont rares, comme un espace d'intégration très large. TensorFlow prend en charge tf.sparse.SparseTensor et les opérations associées pour stocker efficacement les données éparses.

Un tf.SparseTensor , forme : [3, 4]
Une grille 3x4, avec des valeurs dans seulement deux des cellules.
# Sparse tensors store values by index in a memory-efficient manner
sparse_tensor = tf.sparse.SparseTensor(indices=[[0, 0], [1, 2]],
                                       values=[1, 2],
                                       dense_shape=[3, 4])
print(sparse_tensor, "\n")

# You can convert sparse tensors to dense
print(tf.sparse.to_dense(sparse_tensor))

SparseTensor(indices=tf.Tensor(
[[0 0]
 [1 2]], shape=(2, 2), dtype=int64), values=tf.Tensor([1 2], shape=(2,), dtype=int32), dense_shape=tf.Tensor([3 4], shape=(2,), dtype=int64)) 

tf.Tensor(
[[1 0 0 0]
 [0 0 2 0]
 [0 0 0 0]], shape=(3, 4), dtype=int32)