![微分不可能な最適化
目的関数の値しかわからない場合の最適化
2014年11月29日
TokyoWebMining #40
21
シンプレックス法 [Nelder+ 1965]
最適化する空間の次元より1つ多い多面体を使って最適化
4つの操作で、どんどん良い解を見つけていく。通称アメーバ法
2次元上の最適化なら、3点の目的関数値を計算して・・・
鏡映
拡張
収縮
縮小](https://image.slidesharecdn.com/random-141128225344-conversion-gate02/85/-21-320.jpg)
![（参考） 線形方程式解法としての共役勾配法
共役勾配法は元は線形方程式の解法として登場 [Hestenes+ 1952]
TokyoWebMining #40 32 2014年11月29日
を解きたい。
n次元正定値行列
を解くのと等価
共役勾配を使えば、反復解法なのに
有限回の反復で厳密解が求まることを発見
世界に激震が走ったらしい](https://image.slidesharecdn.com/random-141128225344-conversion-gate02/85/-32-320.jpg)
最適化超入門
- 1. 最適化超入門 @tkm2261 TokyoWebMining #40 2014年11月29日 TokyoWebMining #40 1
- 2. 過去の発表 2014年11月29日 TokyoWebMining #40 2 専門と一切関係ナシ 2chテキストマイニングとまとめサイトの自動生成 セクシー女優で学ぶ画像分類入門
- 3. 所属 自己紹介 2014年11月29日 TokyoWebMining #40 3 Twitter ID ｔｋｍ２２６１ 専門 経営工学/最適化 某データ分析会社 業務 分析何でも屋さん 機械学習との出会い 当時の研究が実用性 皆無 精神の逃げ道として 機械学習 を開始 研究が 詰んで、 趣味が本職に 言語、画像と幅広く 遊んでます
- 4. 趣味：自転車 ツールド東北公式トップにちゃっかり載りました 2014年11月29日 TokyoWebMining #40 4
- 5. 趣味：燻製 2014年11月29日 TokyoWebMining #40 5 家が川の近くなので、趣味に
- 6. 最適化ってすごいの？ 『機械学習の学習 ≒ 最適化』の場合がほとんど 2014年11月29日 TokyoWebMining #40 6 最尤推定 （尤度関数最大化） 主成分分析 （分散最大化） サポートベクターマシン （マージン最大化） 協調フィルタリング （Nuclearノルム最小化等）
- 7. 最適化ってすごいの？ データ分析のお仕事でも・・・ 2014年11月29日 TokyoWebMining #40 7 納品物 ： レポート アクション： 提案はするが・・・ 納品物 ： 施策 （レポートも） アクション： 即実行 施策まで落ちるとクライアントも本気 分析のみ 分析 ＋ 最適化
- 8. じゃあ何でみんなやらないの？ 『他分野に溶け込んでる』説 - 機械学習の様にあえて最適化だけをあまり意識しない 『世に出てこない』説 - 最適化は業務と密接に関わるため発表しにくい 『最近まで解けなかった』説 - 業務レベルの最適化は基本NP困難 - 最近はマシンパワーで解けてしまう 『人がいない』説 - 今まで解けなかったので、工学的に最適化できる人が少ない 2014年11月29日 TokyoWebMining #40 8
- 9. 『最適化したい！』と思った時に、 最初に参考になりそうなものを語ります 2014年11月29日 TokyoWebMining #40 9 とりあえず、『人がいない』説の撲滅支援のため、
- 10. が ・ ・ ・ 2014年11月29日 TokyoWebMining #40 10
- 11. 資料作りすぎた 2014年11月29日 TokyoWebMining #40 11 再勉強も兼ねてまとめてたら
- 12. 残り約70ページ 2014年11月29日 TokyoWebMining #40 12
- 13. ・ ・ ・ 2014年11月29日 TokyoWebMining #40 13
- 14. 適度に飛ばすので 気になる箇所は適宜質問 お願いします 2014年11月29日 TokyoWebMining #40 14
- 15. 目次 １．最適化チートシート ２．連続最適化 ２－１．制約なし ２－１－１. 微分情報なし ２－１－２. 微分情報あり ３．組合せ解法 ３－１. メタ解法 ３－２．混合整数計画法 ３－３．制約プログラミング 2014年11月29日 TokyoWebMining #40 15
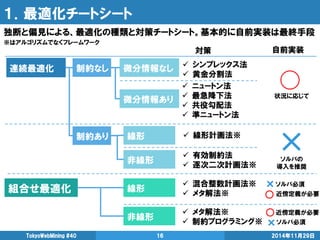
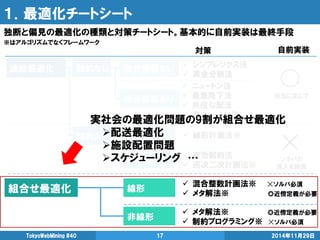
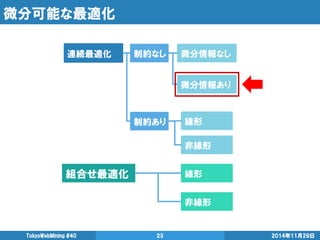
- 16. １．最適化チートシート 2014年11月29日 TokyoWebMining #40 16 連続最適化 組合せ最適化 制約なし 制約あり 微分情報なし 微分情報あり 線形 非線形 線形 非線形 自前実装 対策 シンプレックス法 黄金分割法 ニュートン法 最急降下法 共役勾配法 準ニュートン法 線形計画法※ 有効制約法 逐次二次計画法※ 混合整数計画法※ ソルバ必須 メタ解法※ 近傍定義が必要 メタ解法※ 近傍定義が必要 制約プログラミング※ ソルバ必須 状況に応じて ソルバの 導入を推奨 独断と偏見による、最適化の種類と対策チートシート。基本的に自前実装は最終手段 ※はアルゴリズムでなくフレームワーク
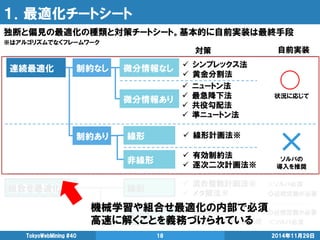
- 17. １．最適化チートシート 2014年11月29日 TokyoWebMining #40 17 連続最適化 組合せ最適化 制約なし 制約あり 微分情報なし 微分情報あり 線形 非線形 線形 非線形 自前実装 対策 シンプレックス法 黄金分割法 ニュートン法 最急降下法 共役勾配法 準ニュートン法 線形計画法※ 有効制約法 逐次二次計画法※ 混合整数計画法※ ☓ソルバ必須 メタ解法※ ◎近傍定義が必要 メタ解法※ ◎近傍定義が必要 制約プログラミング※ ☓ソルバ必須 状況に応じて ソルバの 導入を推奨 独断と偏見の最適化の種類と対策チートシート。基本的に自前実装は最終手段 ※はアルゴリズムでなくフレームワーク 実社会の最適化問題の9割が組合せ最適化 配送最適化 施設配置問題 スケジューリング …
- 18. １．最適化チートシート 2014年11月29日 TokyoWebMining #40 18 連続最適化 組合せ最適化 制約なし 制約あり 微分情報なし 微分情報あり 線形 非線形 線形 非線形 自前実装 対策 シンプレックス法 黄金分割法 ニュートン法 最急降下法 共役勾配法 準ニュートン法 線形計画法※ 有効制約法 逐次二次計画法※ 混合整数計画法※ ☓ソルバ必須 メタ解法※ ◎近傍定義が必要 メタ解法※ ◎近傍定義が必要 制約プログラミング※ ☓ソルバ必須 独断と偏見の最適化の種類と対策チートシート。基本的に自前実装は最終手段 ※はアルゴリズムでなくフレームワーク 合せ最適化 機械学習や組合せ最適化の内部で必須 高速に解くことを義務づけられている 状況に応じて ソルバの 導入を推奨
- 19. ２．連続最適化 2014年11月29日 TokyoWebMining #40 19 アルゴリズムの話メインなので、 実務的な最適化に興味がある方は、組合せ最適化まで飛ばしてください。
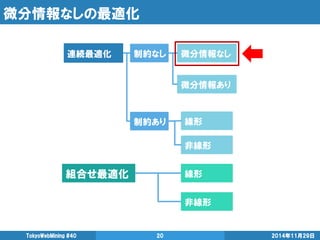
- 20. 微分情報なしの最適化 2014年11月29日 TokyoWebMining #40 20 連続最適化 組合せ最適化 制約なし 制約あり 微分情報なし 微分情報あり 線形 非線形 線形 非線形
- 21. 微分不可能な最適化 目的関数の値しかわからない場合の最適化 2014年11月29日 TokyoWebMining #40 21 シンプレックス法 [Nelder+ 1965] 最適化する空間の次元より1つ多い多面体を使って最適化 4つの操作で、どんどん良い解を見つけていく。通称アメーバ法 2次元上の最適化なら、3点の目的関数値を計算して・・・ 鏡映 拡張 収縮 縮小
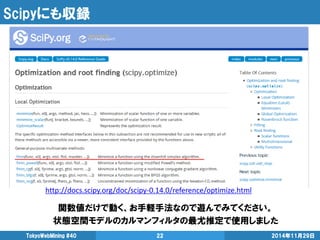
- 22. Scipyにも収録 2014年11月29日 TokyoWebMining #40 22 関数値だけで動く、お手軽手法なので遊んでみてください。 状態空間モデルのカルマンフィルタの最尤推定で使用しました http://docs.scipy.org/doc/scipy-0.14.0/reference/optimize.html
- 23. 微分可能な最適化 2014年11月29日 TokyoWebMining #40 23 連続最適化 組合せ最適化 制約なし 制約あり 微分情報なし 微分情報あり 線形 非線形 線形 非線形
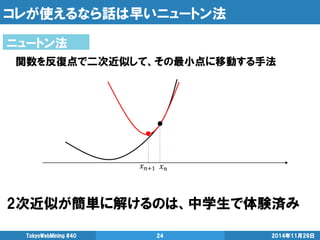
- 24. コレが使えるなら話は早いニュートン法 2次近似が簡単に解けるのは、中学生で体験済み 2014年11月29日 TokyoWebMining #40 24 ニュートン法 関数を反復点で二次近似して、その最小点に移動する手法
- 25. コレが使えるなら話は早いニュートン法 2014年11月29日 TokyoWebMining #40 25 高速に収束（2次収束） - ニュートン法が使える問題ならニュートン法で問題ない ヘッセ行列の逆行列の計算及び保持が必要 - 近年の大規模な問題ではメモリ的に使えない場面が多い - そのため機械学習では1次解法がメイン 降下方向を生成しないことがある。（ 修正ニュートン法） 利点 欠点
- 26. （参考）ニュートン法の表記 検索するとニュートン法の反復式が2種類出てくるが本質は同じ TokyoWebMining #40 26 2014年11月29日 求根アルゴリズムとしてのニュートン法 最適化アルゴリズムとしてのニュートン法 を求めるニュートン法の反復式は を求めるニュートン法の反復式は とすれば両者は一致。つまり停留点を求めている
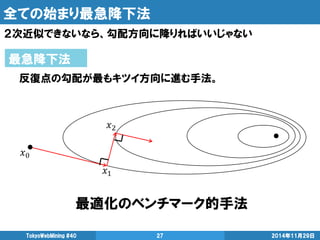
- 27. 全ての始まり最急降下法 ２次近似できないなら、勾配方向に降りればいいじゃない 2014年11月29日 TokyoWebMining #40 27 最急降下法 反復点の勾配が最もキツイ方向に進む手法。 最適化のベンチマーク的手法
- 28. 全ての始まり最急降下法 ２次近似できないなら、勾配方向に降りればいいじゃない 2014年11月29日 TokyoWebMining #40 28 最急降下法 勾配ベクトルだけで動く。実装が簡単。省メモリ 利点 欠点 他手法に比べると収束が遅い （経路がジグザグ） 直線探索が必要
- 29. 直線探索（ラインサーチ）について 2014年11月29日 TokyoWebMining #40 29 方向が決まっても、どこまで行けばよいの？ 直線探索（ラインサーチ） 探索方向のステップサイズを変数とする、一次元最適化問題 機械学習分野では学習率(learning rate)と言われることも ステップサイズ
- 30. 直線探索（ラインサーチ）について 2014年11月29日 TokyoWebMining #40 30 方向が決まっても、どこまで行けばよいの？ 方法１： 厳密に解く 基本出来ないことが多い 方法２： 運を天に任せる 最近のDeep Learning界隈では学習率0.1固定をよく見る 方法３： 収束性が保証されてる、先行研究を使う Armijo条件 （Scipy実装の挙動がおかしいので後述の数値実験では自前実装） Wolfe条件 直線探索（ラインサーチ）
- 31. 共役勾配法 勾配だけでも、もう少し工夫したい 2014年11月29日 TokyoWebMining #40 31 共役勾配法 引用： http://ja.wikipedia.org/wiki/%E5%85%B1%E5%BD%B9%E5%8B%BE%E9%85%8D%E6%B3%95 理論的に超絶美しいが、割愛。実装も簡単 現象面だけに着目すると、 過去の探索方向を考慮に入れた探索方向を生成するので、 ジグザグが緩和される手法 緑線：最急降下法 赤線：共役勾配法
- 32. （参考） 線形方程式解法としての共役勾配法 共役勾配法は元は線形方程式の解法として登場 [Hestenes+ 1952] TokyoWebMining #40 32 2014年11月29日 を解きたい。 n次元正定値行列 を解くのと等価 共役勾配を使えば、反復解法なのに 有限回の反復で厳密解が求まることを発見 世界に激震が走ったらしい
- 33. （参考） 線形方程式解法としての共役勾配法 行列の疎性を効率的に利用可能 - 大規模線形方程式が解ける 実装も簡単 2014年11月29日 TokyoWebMining #40 33 大規模線形方程式の解が、多少精度悪くても必要な場合に有効 リコメンドアルゴリズム等でも使われている 利点 欠点 数値誤差で、有限回の反復で収束しない 固有値の分布で収束性が激変 - 前処理地獄に陥ることも リンク伝播法：リンク予測のための半教師付き学習法 (http://www.geocities.jp/kashi_pong/publication/FPAI73.pdf)
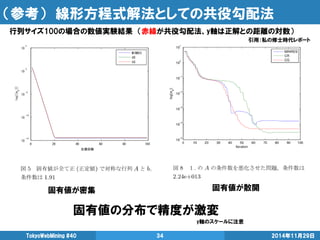
- 34. （参考） 線形方程式解法としての共役勾配法 行列サイズ100の場合の数値実験結果 （赤線が共役勾配法、y軸は正解との距離の対数） 2014年11月29日 TokyoWebMining #40 34 固有値が密集 固有値が散開 固有値の分布で精度が激変 y軸のスケールに注意 引用：私の修士時代レポート
- 35. （参考） 線形方程式解法としての共役勾配法 Scipyにもたくさん実装されている。 （http://docs.scipy.org/doc/scipy-0.14.0/reference/sparse.linalg.html#module-scipy.sparse.linalg） 2014年11月29日 TokyoWebMining #40 35 Q: Aが正定値行列じゃないと解けないの？ A: Krylov部分空間法として一般化されている Q: 一般の最適化問題に共役勾配法使って良いの？ A： 良いが、もちろん有限回の反復で収束しません 直線探索も基本的に必要 Fletcher–Reeves法や Polak–Ribiere法などがあります
- 36. ヘッセ行列よ再び、準ニュートン法 それでもヘッセ行列への夢は捨てられない 2014年11月29日 TokyoWebMining #40 36 準ニュートン法 反復を重ねながらヘッセ行列の逆行列を近似していく手法 ヘッセ行列の逆行列の仕方で、いくつかの派生が存在 •DFP法 •BFGS法（Scipyに実装） 収束が早い（超１次収束） 逆行列計算はないが、 n×n行列を保持する必要がある 利点 欠点
- 37. 結局何を使えばいいの？ 2014年11月29日 TokyoWebMining #40 37 その他にも色々あります。 Deep LearningのライブラリのあるH20では Nesterovの加速勾配法（１次解法）を使っていたりします 語弊を恐れずにまとめると、こんな感じ 手法 収束性 メモリ ニュートン法 ◎ ☓ 準ニュートン法 ○ △ 共役勾配法 △ ○ 最急降下法 ☓ ◎ 試す順番
- 38. 数値実験 TokyoWebMining #40 38 2014年11月29日 Aが2次元正定値行列の以下の問題を各手法で解いた結果 凸2次関数の最適化なので、ニュートン法と共役勾配法に有利な結果
- 39. 2014年11月29日 TokyoWebMining #40 39 微分情報マジ大事 コードは、githubで共有中 https://github.com/anaguma2261/TokyoWebmining_40_tkm2261
- 40. 2014年11月29日 TokyoWebMining #40 40 連続最適化 組合せ最適化 制約なし 制約あり 微分情報なし 微分情報あり 線形 非線形 線形 非線形
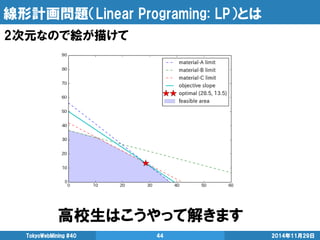
- 41. 線形計画問題（Linear Programing: LP）とは 線形の制約と、線形の目的関数で構成される問題 TokyoWebMining #40 41 2014年11月29日 センター試験や基本情報技術者試験でもお馴染み
- 42. 線形計画問題（Linear Programing: LP）とは 原料種類 製品A 製品B 使用可能量 原料A 12 8 450kg 原料B 3 6 220kg 原料C 10 10 420kg 2014年11月29日 TokyoWebMining #40 42 製品A の利益(万円/kg) 製品B の利益(万円/kg) 8 13 製品Aと製品Bを作るのに必要な材料と使用可能量が以下で 製品Aと製品Bの利益が以下のとき、 利益の最大になるのは、どのような製造量か？
- 43. 線形計画問題（Linear Programing: LP）とは 2014年11月29日 TokyoWebMining #40 43 式で表すと、こんな風に表現できる。
- 44. 線形計画問題（Linear Programing: LP）とは 2014年11月29日 TokyoWebMining #40 44 2次元なので絵が描けて 高校生はこうやって解きます
- 45. 大人はどう解くかというと・・・ STEP1： 最適化モデリング言語を使ってモデル化 有償ソルバにはPython、R、MATLABのものがだいたい付属 STEP2: 線形計画ソルバーに解いてもらう ※混合整数計画ソルバと大体同じなので、後述 2014年11月29日 TokyoWebMining #40 45 MCMCの STANみた いな感じ AMPL 有償の最適化モデリング専用言語。 Pythonでのモデリングが主流になってからは下火 PuLP 無償のPythonの最適化モデリングモジュール 今回はこれでサンプルを作成。 Pythonで出来るのが最大の利点だが、商用利用に不安アリ JuliaOpt 最近出てきたJuliaの最適化モデリングモジュール。無償 MITのチームが頑張って開発しているらしく、今後に期待 自前実装は、 やらないほ うが無難
- 46. 例によって公開中 2014年11月29日 TokyoWebMining #40 46 PuLPとCBCが必須です PuLPはpipで CBCはWindowsはバイナリがあります https://github.com/anaguma2261/TokyoWebmining_40_tkm2261
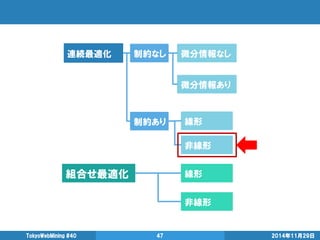
- 47. 2014年11月29日 TokyoWebMining #40 47 連続最適化 組合せ最適化 制約なし 制約あり 微分情報なし 微分情報あり 線形 非線形 線形 非線形
- 48. 凸二次計画問題が限界 非線形の世界でスッキリ解けるのは凸二次計画問題のみ TokyoWebMining #40 48 2014年11月29日 凸二次計画問題 有効制約法や内点法で解くことが可能 無償ソルバーが少ないのが難点。PythonだとCVXOPTぐらい ※Qは正定値行列 目的関数が凸2次関数、制約が線形の問題 2次錐計画問題、半正定値計画問題も無くはないが・・・
- 49. 応用例 TokyoWebMining #40 49 2014年11月29日 分散を最小化 投資比率は足して１ 最低これだけは儲けてね 空売り禁止 ポートフォリオ最適化（平均分散モデル） サポートベクターマシン（SVM）
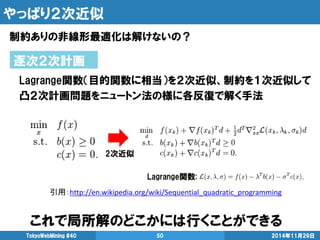
- 50. やっぱり２次近似 制約ありの非線形最適化は解けないの？ 2014年11月29日 TokyoWebMining #40 50 逐次２次計画 Lagrange関数（目的関数に相当）を２次近似、制約を１次近似して 凸２次計画問題をニュートン法の様に各反復で解く手法 引用：http://en.wikipedia.org/wiki/Sequential_quadratic_programming 2次近似 Lagrange関数: これで局所解のどこかには行くことができる
- 51. ３．組合せ解法 2014年11月29日 TokyoWebMining #40 51
- 52. 2014年11月29日 TokyoWebMining #40 52 ３－１. メタ解法
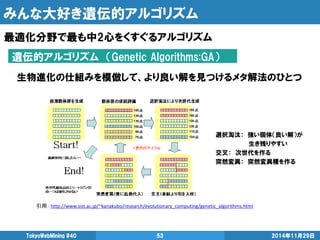
- 53. みんな大好き遺伝的アルゴリズム 最適化分野で最も中2心をくすぐるアルゴリズム 2014年11月29日 TokyoWebMining #40 53 遺伝的アルゴリズム （Genetic Algorithms:GA） 生物進化の仕組みを模倣して、より良い解を見つけるメタ解法のひとつ 引用： http://www.sist.ac.jp/~kanakubo/research/evolutionary_computing/genetic_algorithms.html 選択淘汰： 強い個体（良い解）が 生き残りやすい 交叉： 次世代を作る 突然変異： 突然変異種を作る
- 54. メタ解法とは 組合せ最適化に対する汎用的な発見的解法(精度保証ナシ) 2014年11月29日 TokyoWebMining #40 54 基本的に２つの部品で構成 遺伝的アルゴリズムを強引にあてはめると （GAは若干特殊ケース） 近傍探索 （ローカルサーチ） 突然変異 交叉 解の更新戦略 選択淘汰 近傍探索 （ローカルサーチ） 現在の解の周り（近傍）に良い解がないか探索 解の更新戦略 近傍探索で見つかった解のどこに移動するか ※普通は近傍探索には含まない
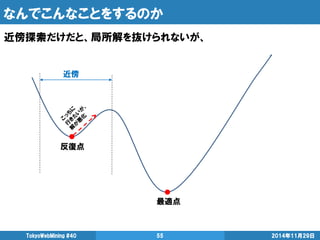
- 55. なんでこんなことをするのか 2014年11月29日 TokyoWebMining #40 55 近傍探索だけだと、局所解を抜けられないが、 最適点 反復点 近傍
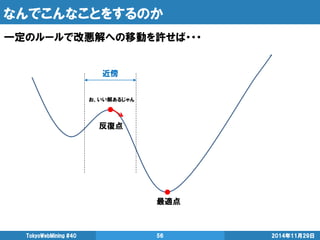
- 56. なんでこんなことをするのか 2014年11月29日 TokyoWebMining #40 56 一定のルールで改悪解への移動を許せば・・・ 最適点 反復点 近傍 お、いい解あるじゃん
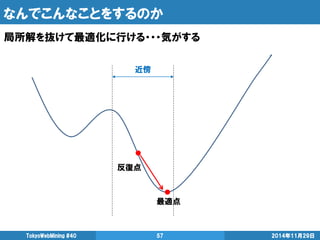
- 57. なんでこんなことをするのか 2014年11月29日 TokyoWebMining #40 57 局所解を抜けて最適化に行ける・・・気がする 最適点 反復点 近傍
- 58. 解の更新戦略による手法のバリエーション 2014年11月29日 TokyoWebMining #40 58 解の更新戦略 遺伝的アルゴリズム（GA） 選択淘汰 タブーサーチ （TS） 過去に行った解には一定期間行かない シミュレーテッド アニーリング法 （SA） 確率的に改悪解への移動を許可する。 メタ解法は挙げると切りがないので、主要３手法のみ紹介
- 59. メタ解法の独断と偏見による考察 2014年11月29日 TokyoWebMining #40 59 遺伝的アルゴリズム （GA） 解をたくさん保持するので、 多様な解を得られるがメモリを喰う 手順が多いのでパラメータが多く調整が大変 解がバイナリ列なら、先行研究が多い タブーサーチ （TS） シンプルでクライアントに説明しやすい 過去の解の持ち方に工夫が必要 シミュレーテッド アニーリング法 （SA） 最適解への収束性を確率的に保証できる優等生 現在解と最良解しか持たないのでメモリに優しい パラメータが少ないので実装簡単 ランダムネスを含んでいるので敬遠することも
- 60. 近傍探索について かなり、問題に依存します 制約が多い場合、 実行可能解を見つけるだけでも大変なことも その時は、混合整数計画法か制約プログラミング 2014年11月29日 TokyoWebMining #40 60
- 61. 2014年11月29日 TokyoWebMining #40 61 ３－２．混合整数計画法
- 62. 混合整数計画法（Mixed Integer Programming：MIP） 線形計画問題に整数制約が追加 TokyoWebMining #40 62 2014年11月29日 メタ解法と異なり、最適性といった解の評価ができる
- 63. 混合整数計画法（Mixed Integer Programming：MIP） 2014年11月29日 TokyoWebMining #40 63 大体NP困難なのを計算力でねじ伏せているのが現状 絶対に自前実装はやめましょう 気になる方は、分枝限定法、切除平面法などをググって下さい。
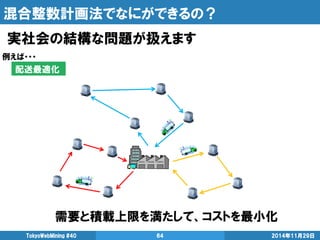
- 64. 混合整数計画法でなにができるの？ 実社会の結構な問題が扱えます TokyoWebMining #40 64 2014年11月29日 配送最適化 需要と積載上限を満たして、コストを最小化 例えば・・・
- 65. 配送最適化の定式化 TokyoWebMining #40 65 2014年11月29日 次数制約１ 次数制約２ トラックの台数 部分巡回路除去制約 積載容量制約 数式乱舞。おかげ様で就職してもTex御用達
- 66. もろもろ定義 2014年11月29日 TokyoWebMining #40 66
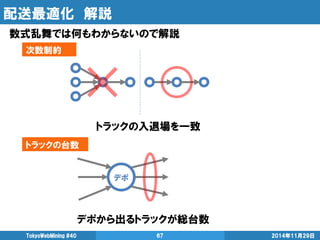
- 67. 配送最適化 解説 数式乱舞では何もわからないので解説 2014年11月29日 TokyoWebMining #40 67 次数制約 トラックの入退場を一致 トラックの台数 デポ デポから出るトラックが総台数
- 68. 配送最適化 解説 TokyoWebMining #40 68 2014年11月29日 部分巡回路除去制約 この定式化の肝、 次数制約だけではデポを含まないルート（部分巡回路）を生成 積載量を単調増加させてデポ以外でルートを作れなくする しかし、混合整数計画法ではIF文を扱えないのでBigM法を使う ※BigM法はデメリットも大きいので用法用量を守りましょう
- 69. 様々な問題を扱える混合整数計画法ですが、 定式化にはセンスと経験が必要 2014年11月29日 TokyoWebMining #40 69
- 70. 参考となる定式化 2014年11月29日 TokyoWebMining #40 70 そんなこと言っていても何も始まらないので 独断と偏見で、知っておくと応用範囲の広い定式化を紹介 配送最適化 次数制約など、ネットワーク上の定式化を理解出来る。 部分巡回路除去制約も時間の制約に拡張できる これが分かれば施設配置問題も楽勝 集合被覆問題 いろんなパーツを使って全体をカバーする感覚が需要 少し、工夫するとそのままシフトスケジューリングになる。
- 71. ソルバーについて 基本的に線形計画問題と同じ手続き 2014年11月29日 TokyoWebMining #40 71 STEP1： 最適化モデリング言語を使ってモデル化 ※P.45参照 STEP2: 混合整数計画ソルバーに解いてもらう
- 72. ソルバーについて 2014年11月29日 TokyoWebMining #40 72 GLPK GPLライセンスのソルバーため商用でも使い難く、最遅ソルバーの呼び声も高い。 ただし、導入の容易性、AMPLファイルが扱える、日本語の資料が豊富などの利点があり、 授業でも使われることも多く、一定の市民権を得ている CBC （CoinMP） Coin-ORというIBMのオペレーションズ・リサーチのオープンソースプロジェクトの一つ CPLライセンスのため商用利用できて、かつ速度もそこそこなので、よく用いられる 欠点としては、英語ですらドキュメントが皆無 SCIP 一応、無料ソルバーでは最速と言われている。 しかし、ZIB Academic Licenseという商用不可のライセンスのため、 使っているところはほとんど見ない。 アカデミックならGurobiもCPLEXもタダで使えるし・・・ 無料ソルバー
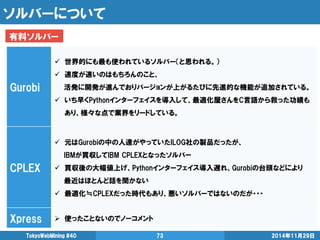
- 73. ソルバーについて 2014年11月29日 TokyoWebMining #40 73 Gurobi 世界的にも最も使われているソルバー（と思われる。） 速度が速いのはもちろんのこと、 活発に開発が進んでおりバージョンが上がるたびに先進的な機能が追加されている。 いち早くPythonインターフェイスを導入して、最適化屋さんをC言語から救った功績も あり、様々な点で業界をリードしている。 CPLEX 元はGurobiの中の人達がやっていたILOG社の製品だったが、 IBMが買収してIBM CPLEXとなったソルバー 買収後の大幅値上げ、Pythonインターフェイス導入遅れ、Gurobiの台頭などにより 最近はほとんど話を聞かない 最適化≒CPLEXだった時代もあり、悪いソルバーではないのだが・・・ Xpress 使ったことないのでノーコメント 有料ソルバー
- 74. 最適化の実務的な注意点 出来るところのテストは徹底 - 最適化自体の単体テストは非常に難しい - 入力の集合や定数、変数数、制約数など出来る限りはテストする 初期解の算段をつけておく - MIPのみだと、妥当な計算時間で解を出さないことがある - 提案時にはわからないことが多いので、初期解を保険とする - 初期解をメタ解法、探索をMIPはよく行われる 2014年11月29日 TokyoWebMining #40 74
- 75. 最適化の実務的な注意点 2014年11月29日 TokyoWebMining #40 75 優秀なエンジニアを早めに味方につけておく - 最適化案件は上手く行けば行くほどツール化の話になります - 最適化は時間がかかるため、ジョブの管理や 『以前の解を保存→初期解として利用』など高度なことが要求されます - 設計だけでも相談しておくと、後々の大事故を防げます お客様は待ってくれない - 最適化屋さんは平気で１時間、１日単位の計算をするが、 お客様はボタン押したら結果がポンっと出てくると考えている - 想定１分、待って５分といったところ - 数時間が許される案件もあるが、 早めに認識を合わせて置かないと大事故につながる
- 76. 2014年11月29日 TokyoWebMining #40 76 ３－３．制約プログラミング
- 77. 制約プログラミング（Constraint Programming： CP） 2014年11月29日 TokyoWebMining #40 77 制約と変数の範囲を与えると、効率良く列挙するフレームワーク ソルバーが少ないのもあり利用例が少ないが、陽の目を見て欲しい手法 利点 欠点 ・ 変数の掛け算（非線形）、論理式制約なんでもゴザレ ・ 最適性の保証はないが、ライブラリによっては オプション一つでメタ解法を使えることもあり、かなり便利 ・ 基本的に変数の範囲を離散値で指定する必要がある ・ ソルバーが少ない
- 78. 制約プログラミング（Constraint Programming： CP） 2014年11月29日 TokyoWebMining #40 78 IBM ILOG CP CPLEXと同じ元ILOG社の製品 使ったことないのでノーコメント 有償 Google CP Solver ILOG社がIBMに買収された時に、CPソルバーチームがGoogleに移籍して開発 使い勝手は結構良かったが、インストールに苦労した記憶がある 無償 SCOP HPがぐぐっても見つからない・・・久保先生に問い合わせる必要があるかも CPソルバー 混合整数計画と解く手続きはほぼ同じ（モデリング＋求解）
- 79. 快適な最適化ライフをお楽しみ下さい ご清聴ありがとうございました 2014年11月29日 TokyoWebMining #40 79
- 80. 参考文献 1.久保幹雄 , 田村明久 , 松井知己. 『応用数理計画ハンドブック』. 朝倉書店. 2002 2.久保幹雄, J. P. ペドロソ, 村松正和, アブドル・レイス. 『あたらしい数理最適化』. 近代科学社. 2012 3.久保 幹雄, J. P. ペドロソ. 『メタヒューリスティクスの数理』. 共立出版 2009 4.柳浦 睦憲, 茨木 俊秀. 『組合せ最適化―メタ戦略を中心として』. 朝倉書店 2001 5.D. G. Luenberger, Y. Ye. 『Linear and Nonlinear Programming』. Springer. 2008 6.小島 政和, 笹島 和幸, 天谷 賢治, 福田 光浩. 『計算機支援数理』. http://www.ocw.titech.ac.jp/index.php?module=General&action=T0300& GakubuCD=226&GakkaCD=226715&KougiCD=75001&Nendo=2011&Gakki=2&lang=JA&vid=05 2014年11月29日 TokyoWebMining #40 80