Postorder Traversal of Binary Tree in Python
Last Updated :
22 Feb, 2025
Postorder traversal is defined as a type of tree traversal which follows the Left-Right-Root policy such that for each node:
- The left subtree is traversed first
- Then the right subtree is traversed
- Finally, the root node of the subtree is traversed
Consider the following tree:

If we perform a postorder traversal in this binary tree, then the traversal will be as follows:
Step-by-step approach:
- Step 1: The traversal will go from 1 to its left subtree i.e., 2, then from 2 to its left subtree root, i.e., 4. Now 4 has no subtree, so it will be visited.
- Step 2: As the left subtree of 2 is visited completely, now it will traverse the right subtree of 2 i.e., it will move to 5. As there is no subtree of 5, it will be visited.
- Step 3: Now both the left and right subtrees of node 2 are visited. So now visit node 2 itself.
- Step 4: As the left subtree of node 1 is traversed, it will now move to the right subtree root, i.e., 3. Node 3 does not have any left subtree, so it will traverse the right subtree i.e., 6. Node 6 has no subtree and so it is visited.
- Step 5: All the subtrees of node 3 are traversed. So now node 3 is visited.
- Step 6: As all the subtrees of node 1 are traversed, now it is time for node 1 to be visited and the traversal ends after that as the whole tree is traversed.
So the order of traversal of nodes is 4 -> 5 -> 2 -> 6 -> 3 -> 1.
Examples of Postorder Traversal
Input:
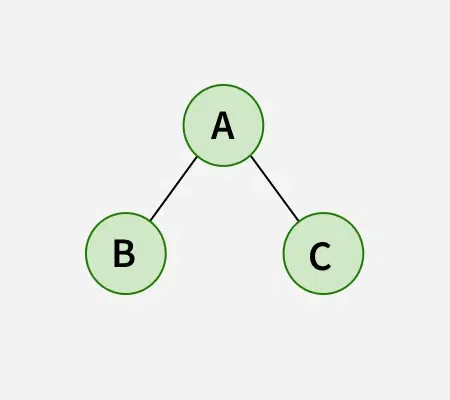
Output: BCA
Explanation: The Post Order Traversal visits the nodes in the following order: Left, Right, Root. Therefore, we visit the left node B, then the right node C and lastly the root node A.
Input:

Output: DEBCA
Input: NULL
Output:
Explanation: Since the tree has no nodes, output is empty in this case.
Algorithm for Postorder Traversal of Binary Tree
The algorithm for postorder traversal is shown as follows:
Postorder(root):
- If root is NULL then return
- Postorder (root -> left)
- Postorder (root -> right)
- Process root (For example, print(root->data))
Python Program to implement Postorder Traversal of Binary Tree
Below is the code implementation of the postorder traversal:
Python
# Python program for postorder traversals
# Structure of a Binary Tree Node
class Node:
def __init__(self, v):
self.data = v
self.left = None
self.right = None
# Function to print postorder traversal
def printPostorder(node):
if node == None:
return
# First recur on left subtree
printPostorder(node.left)
# Then recur on right subtree
printPostorder(node.right)
# Now deal with the node
print(node.data, end=' ')
# Driver code
if __name__ == '__main__':
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.right = Node(6)
# Function call
print("Postorder traversal of binary tree is:")
printPostorder(root)
OutputPostorder traversal of binary tree is:
4 5 2 6 3 1
Complexity Analysis:
Time Complexity: O(n) where n is the total number of nodes. Because it traverses all the nodes at least once.
Auxiliary Space: O(1) if no recursion stack space is considered. Otherwise, O(h) where h is the height of the tree
- In the worst case, h can be the same as n (when the tree is a skewed tree)
- In the best case, h can be the same as log n (when the tree is a complete tree)
Related Posts: