Minimum nodes for same right view in Binary tree

Last Updated : 21 Oct, 2024

Given a binary tree where each node contains a positive integer, the task is to find the minimum number of nodes that need to be removed from the tree, such that the resulting tree has the same right view as the original tree.

Examples:

Input:

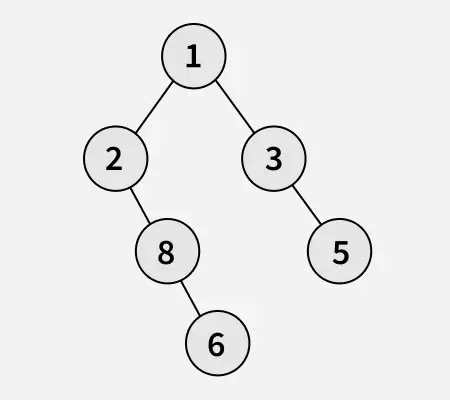
Output: 2
Explanation: The right view of the given binary tree is [1, 3, 5, 6]. If we remove the nodes with values 2, and 8, the resulting tree will also have the same right view as the original tree.
Input:

Output: 3
Explanation: The right view of the original tree is [1, 2, 8, 7]. If we remove the nodes with values 5, 4, and 6, the resulting tree will also have the same right view as the original tree.

Approach:

To maintain the right view of a binary tree, traverse the tree to record the rightmost nodes at each level. Then, recursively count and remove nodes that do not match these rightmost values, ensuring the minimum number of nodes is removed to keep the right view intact.

Steps of the above approach:

Perform a traversal of the tree to identify the rightmost nodes at each level and store their values in a list.
Recursively check each node, counting how many nodes can be removed to maintain the right view based on the previously recorded rightmost values.
For each node, if its left or right child exists, recursively count the removable nodes from those children and compare their values with the rightmost node value at the same level.
Increment the count for any child nodes that do not match the corresponding rightmost node value.
After processing all nodes, return the total count of removable nodes needed to maintain the right view of the tree.

Below is the implementation of the above approach:

C++

// C++ code for the above approach:
#include <bits/stdc++.h>
using namespace std;

class Node {
public:
    int data;
    Node* left;
    Node* right;
    Node(int x) {
      	data = x;
      	left = right = nullptr;
    }
};

// Traverse the tree
void traverse(Node* node, int level, vector<int>& rightmost) {
    if (!node) {
        return;
    }

    if (rightmost.size() == level) {
        rightmost.push_back(node->data);
    }

    traverse(node->right, level + 1, rightmost);
    traverse(node->left, level + 1, rightmost);
}

// Minimum nodes we can remove to keep
// right view same
int countToRemove(Node* node, int level,
                    vector<int>& rightmost) {
    if (!node) {
        return 0;
    }

    int count = 0;

    if (node->left) {
        count += countToRemove(node->left, level + 1,
                                 rightmost);
        if (rightmost[level] != node->data) {
            count++;
        }
    }

    if (node->right) {
        count += countToRemove(node->right, level + 1,
                                 rightmost);
        if (rightmost[level] != node->data) {
            count++;
        }
    }

    // Return the number of nodes that
    // can be removed
    return count;
}

int minNodesToRemove(Node* root) {
    vector<int> rightmost;
    traverse(root, 0, rightmost);
    return countToRemove(root, 0, rightmost);
}

int main() {
    // Construting binary tree.
    //      1
    //     / \
    //    2   3
    //     \   \
    //      8   5
    //       \
    //        6
    
    Node* root = new Node(1);
    root->left = new Node(2);
    root->left->right = new Node(8);
    root->left->right->right = new Node(6);
    root->right = new Node(3);
    root->right->right = new Node(5);

    // Function call
    cout << minNodesToRemove(root) << endl;

    return 0;
}

Java

// Java code to find the minimum number of nodes to remove 
// to keep the right view of a binary tree the same.

import java.util.*;
class Node {
    int data;
    Node left, right;

    Node(int x) {
        data = x;
        left = right = null;
    }
}

class GfG {
    // Traverse the tree
    static void traverse(Node node, int level, List<Integer> rightmost) {
        if (node == null) {
            return;
        }

        if (rightmost.size() == level) {
            rightmost.add(node.data);
        }

        traverse(node.right, level + 1, rightmost);
        traverse(node.left, level + 1, rightmost);
    }

    // Minimum nodes we can remove to keep right view same
    static int countToRemove(Node node, int level, List<Integer> rightmost) {
        if (node == null) {
            return 0;
        }

        int count = 0;

        if (node.left != null) {
            count += countToRemove(node.left, level + 1, rightmost);
            if (rightmost.get(level) != node.data) {
                count++;
            }
        }

        if (node.right != null) {
            count += countToRemove(node.right, level + 1, rightmost);
            if (rightmost.get(level) != node.data) {
                count++;
            }
        }

        // Return the number of nodes that can be removed
        return count;
    }

    static int minNodesToRemove(Node root) {
        List<Integer> rightmost = new ArrayList<>();
        traverse(root, 0, rightmost);
        return countToRemove(root, 0, rightmost);
    }
  
  	public static void main(String[] args) {
        // Constructing binary tree.
        //      1
        //     / \
        //    2   3
        //     \   \
        //      8   5
        //       \
        //        6
        
        Node root = new Node(1);
        root.left = new Node(2);
        root.left.right = new Node(8);
        root.left.right.right = new Node(6);
        root.right = new Node(3);
        root.right.right = new Node(5);

        // Function call
        System.out.println(minNodesToRemove(root));
    }
}

Python

# Python code to find the minimum number of nodes to remove 
# to keep the right view of a binary tree the same.

class Node:
    def __init__(self, x):
        self.data = x
        self.left = None
        self.right = None

def traverse(node, level, rightmost):
    if not node:
        return

    if len(rightmost) == level:
        rightmost.append(node.data)

    traverse(node.right, level + 1, rightmost)
    traverse(node.left, level + 1, rightmost)

# Minimum nodes we can remove to keep right view same
def count_to_remove(node, level, rightmost):
    if not node:
        return 0

    count = 0

    if node.left:
        count += count_to_remove(node.left, level + 1, rightmost)
        if rightmost[level] != node.data:
            count += 1

    if node.right:
        count += count_to_remove(node.right, level + 1, rightmost)
        if rightmost[level] != node.data:
            count += 1

    # Return the number of nodes that can be removed
    return count

def min_nodes_to_remove(root):
    rightmost = []
    traverse(root, 0, rightmost)
    return count_to_remove(root, 0, rightmost)

# Constructing binary tree.
#      1
#     / \
#    2   3
#     \   \
#      8   5
#       \
#        6

root = Node(1)
root.left = Node(2)
root.left.right = Node(8)
root.left.right.right = Node(6)
root.right = Node(3)
root.right.right = Node(5)

# Function call
print(min_nodes_to_remove(root))

// C# code to find the minimum number of nodes to remove 
// to keep the right view of a binary tree the same.

using System;
using System.Collections.Generic;

class Node {
    public int data;
    public Node left, right;

    public Node(int x) {
        data = x;
        left = right = null;
    }
}

class GfG {
    // Traverse the tree
    static void Traverse(Node node, int level, List<int> rightmost) {
        if (node == null) {
            return;
        }

        if (rightmost.Count == level) {
            rightmost.Add(node.data);
        }

        Traverse(node.right, level + 1, rightmost);
        Traverse(node.left, level + 1, rightmost);
    }

    // Minimum nodes we can remove to keep right view same
    static public int CountToRemove(Node node, int level, List<int> rightmost) {
        if (node == null) {
            return 0;
        }

        int count = 0;

        if (node.left != null) {
            count += CountToRemove(node.left, level + 1, rightmost);
            if (rightmost[level] != node.data) {
                count++;
            }
        }

        if (node.right != null) {
            count += CountToRemove(node.right, level + 1, rightmost);
            if (rightmost[level] != node.data) {
                count++;
            }
        }

        // Return the number of nodes that can be removed
        return count;
    }

    static public int MinNodesToRemove(Node root) {
        List<int> rightmost = new List<int>();
        Traverse(root, 0, rightmost);
        return CountToRemove(root, 0, rightmost);
    }
	static void Main(string[] args) {
        // Constructing binary tree.
        //      1
        //     / \
        //    2   3
        //     \   \
        //      8   5
        //       \
        //        6

        Node root = new Node(1);
        root.left = new Node(2);
        root.left.right = new Node(8);
        root.left.right.right = new Node(6);
        root.right = new Node(3);
        root.right.right = new Node(5);

        // Function call
        Console.WriteLine(MinNodesToRemove(root));
    }
}

JavaScript

// JavaScript code to find the minimum number of nodes to remove 
// to keep the right view of a binary tree the same.

class Node {
    constructor(x) {
        this.data = x;
        this.left = this.right = null;
    }
}

function traverse(node, level, rightmost) {
    if (!node) {
        return;
    }

    if (rightmost.length === level) {
        rightmost.push(node.data);
    }

    traverse(node.right, level + 1, rightmost);
    traverse(node.left, level + 1, rightmost);
}

// Minimum nodes we can remove to keep right view same
function countToRemove(node, level, rightmost) {
    if (!node) {
        return 0;
    }

    let count = 0;

    if (node.left) {
        count += countToRemove(node.left, level + 1, rightmost);
        if (rightmost[level] !== node.data) {
            count++;
        }
    }

    if (node.right) {
        count += countToRemove(node.right, level + 1, rightmost);
        if (rightmost[level] !== node.data) {
            count++;
        }
    }

    // Return the number of nodes that can be removed
    return count;
}

function minNodesToRemove(root) {
    let rightmost = [];
    traverse(root, 0, rightmost);
    return countToRemove(root, 0, rightmost);
}

// Constructing binary tree.
//      1
//     / \
//    2   3
//     \   \
//      8   5
//       \
//        6

let root = new Node(1);
root.left = new Node(2);
root.left.right = new Node(8);
root.left.right.right = new Node(6);
root.right = new Node(3);
root.right.right = new Node(5);

// Function call
console.log(minNodesToRemove(root));

Output

Time Complexity: O(n), where n is the number of nodes in the binary tree.
Auxiliary Space: O(h), where h is the height of the binary tree.

Sum of nodes in bottom view of Binary Tree

vishaldhaygude01

Improve

Article Tags :

Practice Tags :

Minimum nodes for same right view in Binary tree

Similar Reads

Thank You!

What kind of Experience do you want to share?