Implementation of Exact Cover Problem and Algorithm X using DLX
Last Updated :
10 Jan, 2023
In the article Exact Cover Problem and Algorithm X | Set 1 we discussed the Exact Cover problem and Algorithm X to solve the Exact cover problem. In this article, we’ll discuss the implementation details of Algorithm X using Dancing Links Technique (DLX) proposed by Dr Donald E. Knuth in his paper “Dancing Links”
Dancing Link Technique
Dancing link technique relies on the idea of doubly circular linked list. As discussed in previous article, we transform exact cover problem in form of matrix of 0 and 1. Here each “1” in the matrix is represented by a node of linked list and the whole matrix is transformed into a mesh of 4 way connected nodes. Each node contains following fields -
- Pointer to node left to it
- Pointer to node right to it
- Pointer to node above it
- Pointer to node below it
- Pointer to list header node to which it belongs
Each row of the matrix is thus a circular linked list linked to each other with left and right pointers and each column of the matrix will also be circular linked list linked to each above with up and down pointer. Each column list also includes a special node called “list header node”. This header node is just like simple node but have few extra fields -
- Column id
- Count of nodes in current column
We can have two different kinds of nodes but in our implementation, we will create only one kind of node with all fields for convenience with an additional “Row id” field which will tell which row this node belongs to. So for matrix -  The 4-way linked matrix will look like this -
The 4-way linked matrix will look like this -
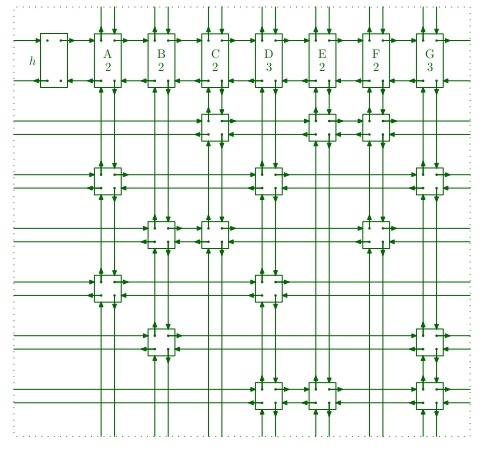 Four way linked matrix
Four way linked matrix
So the pseudo code for search algorithm (Algorithm X) will be -
f( h.right == h ) {
printSolutions();
return;
}
else {
ColumnNode column = getMinColumn();
cover(column);
for( Node row = column.down ; rowNode != column ;
rowNode = rowNode.down ) {
solutions.add( rowNode );
for( Node rightNode = row.right ; rightNode != row ;
rightNode = rightNode.right )
cover( rightNode );
Search( k+1);
solutions.remove( rowNode );
column = rowNode.column;
for( Node leftNode = rowNode.left ; leftNode != row ;
leftNode = leftNode.left )
uncover( leftNode );
}
uncover( column );
} Covering Node
As discussed in the algorithm, we have to remove columns and all the rows to which nodes of that column belongs to. This process is here referred as covering of node. To remove a column we can simply unlink header of that column from neighboring headers. This way this column cannot be accessed. This process is similar to removal of node from doubly linked list, suppose we want to remove node x then -
x.left.right = x.right
x.right.left = x.left
Similarly to remove a row we have to unlink all nodes of row from nodes of row above and below it.
x.up.down = x.down
x.down.up = x.up
Thus the pseudo code for cover(node) becomes -
Node column = dataNode.column;
column.right.left = column.left;
column.left.right = column.right;
for( Node row = column.down ; row != column ; row = row.down )
for( Node rightNode = row.right ; rightNode != row ;
rightNode = rightNode.right ) {
rightNode.up.down = rightNode.down;
rightNode.down.up = rightNode.up;
}
}
So for example, after covering column A, matrix will look like this -
 covering
covering
Here we first remove the column from other columns then we move down to each column node and remove row by traversing right, so row 2 and 4 is removed.
Uncovering Node
Suppose algorithm reached a dead end and no solution is possible in that case algorithm have to backtrack. Because we have removed columns and rows when we backtrack we have link again those removed rows and columns. This is what we are calling uncovering. Notice that the removed nodes still have pointers to their neighbors, so we can link them back again using these pointers. To uncover column we will perform covering operation but in reverse order -
x.left.right = x
x.right.left = x
Similarly to uncover any row node x -
x.up.down = x
x.down.up = x
Thus the pseudo code for uncover(node) will become -
Node column = dataNode.column;
for( Node row = column.up ; row != column ; row = row.up )
for( Node leftNode = row.left ; leftNode != row ;
leftNode = leftNode.right ) {
leftNode.up.down = leftNode;
leftNode.down.up = leftNode;
}
column.right.left = column;
column.left.right = column;
}
Following is the implementation of dancing link technique -
CPP
// C++ program for solving exact cover problem
// using DLX (Dancing Links) technique
#include <bits/stdc++.h>
#define MAX_ROW 100
#define MAX_COL 100
using namespace std;
struct Node
{
public:
struct Node *left;
struct Node *right;
struct Node *up;
struct Node *down;
struct Node *column;
int rowID;
int colID;
int nodeCount;
};
// Header node, contains pointer to the
// list header node of first column
struct Node *header = new Node();
// Matrix to contain nodes of linked mesh
struct Node Matrix[MAX_ROW][MAX_COL];
// Problem Matrix
bool ProbMat[MAX_ROW][MAX_COL];
// vector containing solutions
vector <struct Node*> solutions;
// Number of rows and columns in problem matrix
int nRow = 0,nCol = 0;
// Functions to get next index in any direction
// for given index (circular in nature)
int getRight(int i){return (i+1) % nCol; }
int getLeft(int i){return (i-1 < 0) ? nCol-1 : i-1 ; }
int getUp(int i){return (i-1 < 0) ? nRow : i-1 ; }
int getDown(int i){return (i+1) % (nRow+1); }
// Create 4 way linked matrix of nodes
// called Toroidal due to resemblance to
// toroid
Node *createToridolMatrix()
{
// One extra row for list header nodes
// for each column
for(int i = 0; i <= nRow; i++)
{
for(int j = 0; j < nCol; j++)
{
// If it's 1 in the problem matrix then
// only create a node
if(ProbMat[i][j])
{
int a, b;
// If it's 1, other than 1 in 0th row
// then count it as node of column
// and increment node count in column header
if(i) Matrix[0][j].nodeCount += 1;
// Add pointer to column header for this
// column node
Matrix[i][j].column = &Matrix[0][j];
// set row and column id of this node
Matrix[i][j].rowID = i;
Matrix[i][j].colID = j;
// Link the node with neighbors
// Left pointer
a = i; b = j;
do{ b = getLeft(b); } while(!ProbMat[a][b] && b != j);
Matrix[i][j].left = &Matrix[i][b];
// Right pointer
a = i; b = j;
do { b = getRight(b); } while(!ProbMat[a][b] && b != j);
Matrix[i][j].right = &Matrix[i][b];
// Up pointer
a = i; b = j;
do { a = getUp(a); } while(!ProbMat[a][b] && a != i);
Matrix[i][j].up = &Matrix[a][j];
// Down pointer
a = i; b = j;
do { a = getDown(a); } while(!ProbMat[a][b] && a != i);
Matrix[i][j].down = &Matrix[a][j];
}
}
}
// link header right pointer to column
// header of first column
header->right = &Matrix[0][0];
// link header left pointer to column
// header of last column
header->left = &Matrix[0][nCol-1];
Matrix[0][0].left = header;
Matrix[0][nCol-1].right = header;
return header;
}
// Cover the given node completely
void cover(struct Node *targetNode)
{
struct Node *row, *rightNode;
// get the pointer to the header of column
// to which this node belong
struct Node *colNode = targetNode->column;
// unlink column header from it's neighbors
colNode->left->right = colNode->right;
colNode->right->left = colNode->left;
// Move down the column and remove each row
// by traversing right
for(row = colNode->down; row != colNode; row = row->down)
{
for(rightNode = row->right; rightNode != row;
rightNode = rightNode->right)
{
rightNode->up->down = rightNode->down;
rightNode->down->up = rightNode->up;
// after unlinking row node, decrement the
// node count in column header
Matrix[0][rightNode->colID].nodeCount -= 1;
}
}
}
// Uncover the given node completely
void uncover(struct Node *targetNode)
{
struct Node *rowNode, *leftNode;
// get the pointer to the header of column
// to which this node belong
struct Node *colNode = targetNode->column;
// Move down the column and link back
// each row by traversing left
for(rowNode = colNode->up; rowNode != colNode; rowNode = rowNode->up)
{
for(leftNode = rowNode->left; leftNode != rowNode;
leftNode = leftNode->left)
{
leftNode->up->down = leftNode;
leftNode->down->up = leftNode;
// after linking row node, increment the
// node count in column header
Matrix[0][leftNode->colID].nodeCount += 1;
}
}
// link the column header from it's neighbors
colNode->left->right = colNode;
colNode->right->left = colNode;
}
// Traverse column headers right and
// return the column having minimum
// node count
Node *getMinColumn()
{
struct Node *h = header;
struct Node *min_col = h->right;
h = h->right->right;
do
{
if(h->nodeCount < min_col->nodeCount)
{
min_col = h;
}
h = h->right;
}while(h != header);
return min_col;
}
void printSolutions()
{
cout<<"Printing Solutions: ";
vector<struct Node*>::iterator i;
for(i = solutions.begin(); i!=solutions.end(); i++)
cout<<(*i)->rowID<<" ";
cout<<"\n";
}
// Search for exact covers
void search(int k)
{
struct Node *rowNode;
struct Node *rightNode;
struct Node *leftNode;
struct Node *column;
// if no column left, then we must
// have found the solution
if(header->right == header)
{
printSolutions();
return;
}
// choose column deterministically
column = getMinColumn();
// cover chosen column
cover(column);
for(rowNode = column->down; rowNode != column;
rowNode = rowNode->down )
{
solutions.push_back(rowNode);
for(rightNode = rowNode->right; rightNode != rowNode;
rightNode = rightNode->right)
cover(rightNode);
// move to level k+1 (recursively)
search(k+1);
// if solution in not possible, backtrack (uncover)
// and remove the selected row (set) from solution
solutions.pop_back();
column = rowNode->column;
for(leftNode = rowNode->left; leftNode != rowNode;
leftNode = leftNode->left)
uncover(leftNode);
}
uncover(column);
}
// Driver code
int main()
{
/*
Example problem
X = {1,2,3,4,5,6,7}
set-1 = {1,4,7}
set-2 = {1,4}
set-3 = {4,5,7}
set-4 = {3,5,6}
set-5 = {2,3,6,7}
set-6 = {2,7}
set-7 = {1,4}
Solutions : {6 ,4, 2} and {6, 4, 7}
*/
nRow = 7;
nCol = 7;
// initialize the problem matrix
// ( matrix of 0 and 1) with 0
for(int i=0; i<=nRow; i++)
{
for(int j=0; j<nCol; j++)
{
// if it's row 0, it consist of column
// headers. Initialize it with 1
if(i == 0) ProbMat[i][j] = true;
else ProbMat[i][j] = false;
}
}
// Manually filling up 1's
ProbMat[1][0] = true; ProbMat[1][3] = true;
ProbMat[1][6] = true; ProbMat[2][0] = true;
ProbMat[2][3] = true; ProbMat[3][3] = true;
ProbMat[3][4] = true; ProbMat[3][6] = true;
ProbMat[4][2] = true; ProbMat[4][4] = true;
ProbMat[4][5] = true; ProbMat[5][1] = true;
ProbMat[5][2] = true; ProbMat[5][5] = true;
ProbMat[5][6] = true; ProbMat[6][1] = true;
ProbMat[6][6] = true; ProbMat[7][0] = true;
ProbMat[7][3] = true;
// create 4-way linked matrix
createToridolMatrix();
search(0);
return 0;
}
Output:
Printing Solutions: 6 4 2
Printing Solutions: 6 4 7
The time complexity of the createToridolMatrix() function is O(n^2), where n is the number of rows and columns in the ProbMat array. This is because the function iterates through every element in the ProbMat array and creates a new node for each element that is equal to 1.
The space complexity of the createToridolMatrix() function is also O(n^2), since it creates a new node for each element in the ProbMat array that is equal to 1.
The time and space complexity of the remaining functions in the program depend on the specific implementation of the DLX algorithm and the specific problem being solved. However, in general, the time complexity of the DLX algorithm is exponential in the worst case, although it often performs much better in practice. The space complexity of the DLX algorithm is generally linear in the size of the input.
References
Similar Reads
C++ Programming Language C++ is a computer programming language developed by Bjarne Stroustrup as an extension of the C language. It is known for is fast speed, low level memory management and is often taught as first programming language. It provides:Hands-on application of different programming concepts.Similar syntax to
5 min read
C++ Overview
Introduction to C++ Programming LanguageC++ is a general-purpose programming language that was developed by Bjarne Stroustrup as an enhancement of the C language to add object-oriented paradigm. It is considered as a middle-level language as it combines features of both high-level and low-level languages. It has high level language featur
3 min read
Features of C++C++ is a general-purpose programming language that was developed as an enhancement of the C language to include an object-oriented paradigm. It is an imperative and compiled language. C++ has a number of features, including:Object-Oriented ProgrammingMachine IndependentSimpleHigh-Level LanguagePopul
5 min read
History of C++The C++ language is an object-oriented programming language & is a combination of both low-level & high-level language - a Middle-Level Language. The programming language was created, designed & developed by a Danish Computer Scientist - Bjarne Stroustrup at Bell Telephone Laboratories (
7 min read
Interesting Facts about C++C++ is a general-purpose, object-oriented programming language. It supports generic programming and low-level memory manipulation. Bjarne Stroustrup (Bell Labs) in 1979, introduced the C-With-Classes, and in 1983 with the C++. Here are some awesome facts about C++ that may interest you: The name of
2 min read
Setting up C++ Development EnvironmentC++ runs on lots of platforms like Windows, Linux, Unix, Mac, etc. If you do not want to set up a local environment you can also use online IDEs for compiling your program.Using Online IDEIDE stands for an integrated development environment. IDE is a software application that provides facilities to
8 min read
Difference between C and C++C++ is often viewed as a superset of C. C++ is also known as a "C with class" This was very nearly true when C++ was originally created, but the two languages have evolved over time with C picking up a number of features that either weren't found in the contemporary version of C++ or still haven't m
3 min read
C++ Basics
Understanding First C++ ProgramThe "Hello World" program is the first step towards learning any programming language and is also one of the most straightforward programs you will learn. It is the basic program that demonstrates the working of the coding process. All you have to do is display the message "Hello World" on the outpu
4 min read
C++ Basic SyntaxSyntax refers to the rules and regulations for writing statements in a programming language. They can also be viewed as the grammatical rules defining the structure of a programming language.The C++ language also has its syntax for the functionalities it provides. Different statements have different
4 min read
C++ CommentsComments in C++ are meant to explain the code as well as to make it more readable. Their purpose is to provide information about code lines. When testing alternative code, they can also be used to prevent execution of some part of the code. Programmers commonly use comments to document their work.Ex
3 min read
Tokens in CIn C programming, tokens are the smallest units in a program that have meaningful representations. Tokens are the building blocks of a C program, and they are recognized by the C compiler to form valid expressions and statements. Tokens can be classified into various categories, each with specific r
4 min read
C++ KeywordsKeywords are the reserved words that have special meanings in the C++ language. They are the words that have special meaning in the language. C++ uses keywords for a specifying the components of the language, such as void, int, public, etc. They can't be used for a variable name, function name or an
2 min read
Difference between Keyword and Identifier in CIn C, keywords and identifiers are basically the fundamental parts of the language used. Identifiers are the names that can be given to a variable, function or other entity while keywords are the reserved words that have predefined meaning in the language.The below table illustrates the primary diff
3 min read
C++ Variables and Constants
C++ VariablesIn C++, variable is a name given to a memory location. It is the basic unit of storage in a program. The value stored in a variable can be accessed or changed during program execution.Creating a VariableCreating a variable and giving it a name is called variable definition (sometimes called variable
4 min read
Constants in CIn C programming, const is a keyword used to declare a variable as constant, meaning its value cannot be changed after it is initialized. It is mainly used to protect variables from being accidentally modified, making the program safer and easier to understand. These constants can be of various type
4 min read
Scope of Variables in C++In C++, the scope of a variable is the extent in the code upto which the variable can be accessed or worked with. It is the region of the program where the variable is accessible using the name it was declared with.Let's take a look at an example:C++#include <iostream> using namespace std; //
7 min read
Storage Classes in C++ with ExamplesC++ Storage Classes are used to describe the characteristics of a variable/function. It determines the lifetime, visibility, default value, and storage location which helps us to trace the existence of a particular variable during the runtime of a program. Storage class specifiers are used to specif
6 min read
Static Keyword in C++The static keyword in C++ has different meanings when used with different types. In this article, we will learn about the static keyword in C++ along with its various uses.In C++, a static keyword can be used in the following context:Table of ContentStatic Variables in a FunctionStatic Member Variab
5 min read
C++ Data Types and Literals
C++ Data TypesData types specify the type of data that a variable can store. Whenever a variable is defined in C++, the compiler allocates some memory for that variable based on the data type with which it is declared as every data type requires a different amount of memory.C++ supports a wide variety of data typ
7 min read
Literals in CIn C, Literals are the constant values that are assigned to the variables. Literals represent fixed values that cannot be modified. Literals contain memory but they do not have references as variables. Generally, both terms, constants, and literals are used interchangeably. For example, “const int =
4 min read
Derived Data Types in C++The data types that are derived from the primitive or built-in datatypes are referred to as Derived Data Types. They are generally the data types that are created from the primitive data types and provide some additional functionality.In C++, there are four different derived data types:Table of Cont
4 min read
User Defined Data Types in C++User defined data types are those data types that are defined by the user himself. In C++, these data types allow programmers to extend the basic data types provided and create new types that are more suited to their specific needs. C++ supports 5 user-defined data types:Table of ContentClassStructu
4 min read
Data Type Ranges and Their Macros in C++Most of the times, in competitive programming, there is a need to assign the variable, the maximum or minimum value that data type can hold but remembering such a large and precise number comes out to be a difficult job. Therefore, C++ has certain macros to represent these numbers, so that these can
3 min read
C++ Type ModifiersIn C++, type modifiers are the keywords used to change or give extra meaning to already existing data types. It is added to primitive data types as a prefix to modify their size or range of data they can store.C++ have 4 type modifiers which are as follows:Table of Contentsigned Modifierunsigned Mod
4 min read
Type Conversion in C++Type conversion means converting one type of data to another compatible type such that it doesn't lose its meaning. It is essential for managing different data types in C++. Let's take a look at an example:C++#include <iostream> using namespace std; int main() { // Two variables of different t
4 min read
Casting Operators in C++The casting operators is the modern C++ solution for converting one type of data safely to another type. This process is called typecasting where the type of the data is changed to another type either implicitly (by the compiler) or explicitly (by the programmer).Let's take a look at an example:C++#
5 min read
C++ Operators
Operators in C++C++ operators are the symbols that operate on values to perform specific mathematical or logical computations on given values. They are the foundation of any programming language.Example:C++#include <iostream> using namespace std; int main() { int a = 10 + 20; cout << a; return 0; }Outpu
9 min read
C++ Arithmetic OperatorsArithmetic Operators in C++ are used to perform arithmetic or mathematical operations on the operands (generally numeric values). An operand can be a variable or a value. For example, ‘+’ is used for addition, '-' is used for subtraction, '*' is used for multiplication, etc. Let's take a look at an
4 min read
Unary Operators in CIn C programming, unary operators are operators that operate on a single operand. These operators are used to perform operations such as negation, incrementing or decrementing a variable, or checking the size of a variable. They provide a way to modify or manipulate the value of a single variable in
5 min read
Bitwise Operators in CIn C, bitwise operators are used to perform operations directly on the binary representations of numbers. These operators work by manipulating individual bits (0s and 1s) in a number.The following 6 operators are bitwise operators (also known as bit operators as they work at the bit-level). They are
6 min read
Assignment Operators in CIn C, assignment operators are used to assign values to variables. The left operand is the variable and the right operand is the value being assigned. The value on the right must match the data type of the variable otherwise, the compiler will raise an error.Let's take a look at an example:C#include
4 min read
C++ sizeof OperatorThe sizeof operator is a unary compile-time operator used to determine the size of variables, data types, and constants in bytes at compile time. It can also determine the size of classes, structures, and unions.Let's take a look at an example:C++#include <iostream> using namespace std; int ma
3 min read
Scope Resolution Operator in C++In C++, the scope resolution operator (::) is used to access the identifiers such as variable names and function names defined inside some other scope in the current scope. Let's take a look at an example:C++#include <iostream> int main() { // Accessing cout from std namespace using scope // r
4 min read
C++ Input/Output
C++ Control Statements
Decision Making in C (if , if..else, Nested if, if-else-if )In C, programs can choose which part of the code to execute based on some condition. This ability is called decision making and the statements used for it are called conditional statements. These statements evaluate one or more conditions and make the decision whether to execute a block of code or n
7 min read
C++ if StatementThe C++ if statement is the most simple decision-making statement. It is used to decide whether a certain statement or block of statements will be executed or not executed based on a certain condition. Let's take a look at an example:C++#include <iostream> using namespace std; int main() { int
3 min read
C++ if else StatementThe if statement alone tells us that if a condition is true it will execute a block of statements and if the condition is false, it won’t. But what if we want to do something else if the condition is false. Here comes the C++ if else statement. We can use the else statement with if statement to exec
3 min read
C++ if else if LadderIn C++, the if-else-if ladder helps the user decide from among multiple options. The C++ if statements are executed from the top down. As soon as one of the conditions controlling the if is true, the statement associated with that if is executed, and the rest of the C++ else-if ladder is bypassed. I
3 min read
Switch Statement in C++In C++, the switch statement is a flow control statement that is used to execute the different blocks of statements based on the value of the given expression. It is a simpler alternative to the long if-else-if ladder.SyntaxC++switch (expression) { case value_1: // code to be executed. break; case v
5 min read
Jump statements in C++Jump statements are used to manipulate the flow of the program if some conditions are met. It is used to terminate or continue the loop inside a program or to stop the execution of a function.In C++, there is four jump statement:Table of Contentcontinue Statementbreak Statementreturn Statementgoto S
4 min read
C++ LoopsIn C++ programming, sometimes there is a need to perform some operation more than once or (say) n number of times. For example, suppose we want to print "Hello World" 5 times. Manually, we have to write cout for the C++ statement 5 times as shown.C++#include <iostream> using namespace std; int
7 min read
for Loop in C++In C++, for loop is an entry-controlled loop that is used to execute a block of code repeatedly for the given number of times. It is generally preferred over while and do-while loops in case the number of iterations is known beforehand.Let's take a look at an example:C++#include <bits/stdc++.h
6 min read
Range-Based for Loop in C++In C++, the range-based for loop introduced in C++ 11 is a version of for loop that is able to iterate over a range. This range can be anything that is iteratable, such as arrays, strings and STL containers. It provides a more readable and concise syntax compared to traditional for loops.Let's take
3 min read
C++ While LoopIn C++, the while loop is an entry-controlled loop that repeatedly executes a block of code as long as the given condition remains true. Unlike the for loop, while loop is used in situations where we do not know the exact number of iterations of the loop beforehand as the loop execution is terminate
3 min read
C++ do while LoopIn C++, the do-while loop is an exit-controlled loop that repeatedly executes a block of code at least once and continues executing as long as a given condition remains true. Unlike the while loop, the do-while loop guarantees that the loop body will execute at least once, regardless of whether the
4 min read
C++ Functions
Functions in C++A Function is a reusable block of code designed to perform a specific task. It helps break large programs into smaller, logical parts. Functions make code cleaner, easier to understand, and more maintainable.Just like in other languages, C++ functions can take inputs (called parameters), execute a b
8 min read
return Statement in C++In C++, the return statement returns the flow of the execution to the function from where it is called. This statement does not mandatorily need any conditional statements. As soon as the statement is executed, the flow of the program stops immediately and returns the control from where it was calle
4 min read
Parameter Passing Techniques in CIn C, passing values to a function means providing data to the function when it is called so that the function can use or manipulate that data. Here:Formal Parameters: Variables used in parameter list in a function declaration/definition as placeholders. Also called only parameters.Actual Parameters
3 min read
Difference Between Call by Value and Call by Reference in CFunctions can be invoked in two ways: Call by Value or Call by Reference. These two ways are generally differentiated by the type of values passed to them as parameters.The following table lists the differences between the call-by-value and call-by-reference methods of parameter passing.Call By Valu
4 min read
Default Arguments in C++A default argument is a value provided for a parameter in a function declaration that is automatically assigned by the compiler if no value is provided for those parameters in function call. If the value is passed for it, the default value is overwritten by the passed value.Example:C++#include <i
5 min read
Inline Functions in C++In C++, inline functions provide a way to optimize the performance of the program by reducing the overhead related to a function call. When a function is specified as inline the whole code of the inline function is inserted or substituted at the point of its call during the compilation instead of us
6 min read
Lambda Expression in C++C++ 11 introduced lambda expressions to allow inline functions which can be used for short snippets of code that are not going to be reused. Therefore, they do not require a name. They are mostly used in STL algorithms as callback functions.Example:C++#include <iostream> using namespace std; i
4 min read
C++ Pointers and References
Pointers and References in C++In C++ pointers and references both are mechanisms used to deal with memory, memory address, and data in a program. Pointers are used to store the memory address of another variable whereas references are used to create an alias for an already existing variable. Pointers in C++ Pointers in C++ are a
5 min read
C++ PointersA pointer is a special variable that holds the memory address of another variable, rather than storing a direct value itself. Pointers allow programs to access and manipulate data in memory efficiently, making them a key feature for system-level programming and dynamic memory management. When we acc
8 min read
Dangling, Void , Null and Wild Pointers in CIn C programming pointers are used to manipulate memory addresses, to store the address of some variable or memory location. But certain situations and characteristics related to pointers become challenging in terms of memory safety and program behavior these include Dangling (when pointing to deall
6 min read
Applications of Pointers in CPointers in C are variables that are used to store the memory address of another variable. Pointers allow us to efficiently manage the memory and hence optimize our program. In this article, we will discuss some of the major applications of pointers in C. Prerequisite: Pointers in C. C Pointers Appl
4 min read
Understanding nullptr in C++Consider the following C++ program that shows problem with NULL (need of nullptr) CPP // C++ program to demonstrate problem with NULL #include <bits/stdc++.h> using namespace std; // function with integer argument void fun(int N) { cout << "fun(int)"; return;} // Overloaded fun
3 min read
References in C++In C++, a reference works as an alias for an existing variable, providing an alternative name for it and allowing you to work with the original data directly.Example:C++#include <iostream> using namespace std; int main() { int x = 10; // ref is a reference to x. int& ref = x; // printing v
5 min read
Can References Refer to Invalid Location in C++?Reference Variables: You can create a second name for a variable in C++, which you can use to read or edit the original data contained in that variable. While this may not sound appealing at first, declaring a reference and assigning it a variable allows you to treat the reference as if it were the
2 min read
Pointers vs References in C++Prerequisite: Pointers, References C and C++ support pointers, which is different from most other programming languages such as Java, Python, Ruby, Perl and PHP as they only support references. But interestingly, C++, along with pointers, also supports references. On the surface, both references and
5 min read
Passing By Pointer vs Passing By Reference in C++In C++, we can pass parameters to a function either by pointers or by reference. In both cases, we get the same result. So, what is the difference between Passing by Pointer and Passing by Reference in C++?Let's first understand what Passing by Pointer and Passing by Reference in C++ mean:Passing by
5 min read
When do we pass arguments by pointer?In C, the pass-by pointer method allows users to pass the address of an argument to the function instead of the actual value. This allows programmers to change the actual data from the function and also improve the performance of the program. In C, variables are passed by pointer in the following ca
5 min read