Zech's logarithm
Zech logarithms are used to implement addition in finite fields when elements are represented as powers of a generator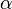 
.
Zech logarithms are named after Julius Zech, and are also called Jacobi logarithms, after C. G. J. Jacobi who used them for number theoretic investigations (C. G. J. Jacoby, "Über die Kreistheilung und ihre Anwendung auf die Zahlentheorie", in Gesammelte Werke, Vol.6, pp. 254–274).
Definition
If 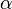is a primitive element of a finite field, then the Zech logarithm relative to the base 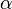is defined by the equation
or equivalently by
The choice of base 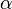is usually dropped from the notation when it's clear from context.
To be more precise, 
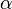is a function on the integers modulo the multiplicative order of , and takes values in the same set. In order to describe every element, it is convenient to formally add a new symbol 
, along with the definitions
where 
is an integer satisfying 
, that is 
for a field of characteristic 2, and 
for a field of odd characteristic with 
elements.
Podcasts:
