Weierstrass function
In mathematics, the Weierstrass function is an example of a pathological real-valued function on the real line. The function has the property of being continuous everywhere but differentiable nowhere. It is named after its discoverer Karl Weierstrass.
Historically, the Weierstrass function is important because it was the first published example (1872) to challenge the notion that every continuous function was differentiable except on a set of isolated points.
Construction
In Weierstrass' original paper, the function was defined as the sum of a Fourier series:
where 
, 
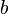is a positive odd integer, and
The minimum value of 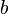which satisfies these constraints is 
. This construction, along with the proof that the function is nowhere differentiable, was first given by Weierstrass in a paper presented to the Königliche Akademie der Wissenschaften on 18 July 1872.
The proof that this function is continuous everywhere is not difficult. Since the terms of the infinite series which defines it are bounded by ±an and this has finite sum for 0 < a < 1, convergence of the sum of the terms is uniform by the Weierstrass M-test with Mn = an. Since each partial sum is continuous and the uniform limit of continuous functions is continuous, it follows f is continuous.
Podcasts:
