Keen

Keen may refer to:

People

Other

Video games

See also

Keen (song)

"Keen" is a 1985 non-album single by That Petrol Emotion.
The 12" B-side "Zig-Zag Wanderer" was originally recorded by Captain Beefheart and his Magic Band in 1967.

Track listing 7"

Side A

"Keen" (John O'Neill) (3:10)

Side B

"A Great Depression On A Slum Night" (John O'Neill) (4:03)

Track listing 12"

Side A

"Keen" (John O'Neill) (3:10)

Side B

"A Great Depression On A Slum Night" (John O'Neill) (4:03)

"Zig-Zag Wanderer" (Don Van Vliet/Herb Bermann) (2:24)

Personnel

References

Suikoden IV

Suikoden IV (Japanese: 幻想水滸伝IV, Hepburn: Gensō Suikoden Fō,  (listen) ) is a role-playing video game developed and published by Konami for the Sony PlayStation 2 video game console and is the fourth installment of the Suikoden video game series. It was released in August 2004 in Japan, and early 2005 in North America and Europe.

Suikoden IV takes place approximately 150 years before the events of the first Suikoden game, and relates the story of a young boy living on the island of Razril and the Rune of Punishment, one of the 27 True Runes. The Rune of Punishment governs both atonement and forgiveness, and is unusual in that it consumes the life of the bearer with use; once the previous bearer dies, it immediately jumps to someone nearby. Meanwhile, the Kooluk Empire seeks to expand into the nearby Island Nations.

Konami later produced Suikoden Tactics, a spinoff that serves as a direct prequel, side-story, and sequel to Suikoden IV.

Gameplay

Chess theory

The game of chess is commonly divided into three phases: the opening, middlegame, and endgame. There is a large body of theory regarding how the game should be played in each of these phases, especially the opening and endgame. Those who write about chess theory, who are often but not necessarily also eminent players, are referred to as "theorists" or "theoreticians".

"Opening theory" commonly refers to consensus, broadly represented by current literature on the openings. "Endgame theory" consists of statements regarding specific positions, or positions of a similar type, though there are few universally applicable principles. "Middlegame theory" often refers to maxims or principles applicable to the middlegame. The modern trend, however, is to assign paramount importance to analysis of the specific position at hand rather than to general principles.

The development of theory in all of these areas has been assisted by the vast literature on the game. In 1913, preeminent chess historian H. J. R. Murray wrote in his 900-page magnum opus A History of Chess that, "The game possesses a literature which in contents probably exceeds that of all other games combined." He estimated that at that time the "total number of books on chess, chess magazines, and newspapers devoting space regularly to the game probably exceeds 5,000". In 1949, B. H. Wood opined that the number had increased to about 20,000.David Hooper and Kenneth Whyld wrote in 1992 that, "Since then there has been a steady increase year by year of the number of new chess publications. No one knows how many have been printed..." The world's largest chess library, the John G. White Collection at the Cleveland Public Library, contains over 32,000 chess books and serials, including over 6,000 bound volumes of chess periodicals. Chess players today also avail themselves of computer-based sources of information.

Theory (mathematical logic)

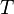In mathematical logic, a theory (also called a formal theory) is a set of sentences in a formal language. Usually a deductive system is understood from context. An element of a theory is then called an axiom of the theory, and any sentence that follows from the axioms () is called a theorem of the theory. Every axiom is also a theorem. A first-order theory is a set of first-order sentences.

Theories expressed in formal language generally

When defining theories for foundational purposes, additional care must be taken and normal set-theoretic language may not be appropriate.

The construction of a theory begins by specifying a definite non-empty conceptual class , the elements of which are called statements. These initial statements are often called the primitive elements or elementary statements of the theory, to distinguish them from other statements which may be derived from them.

A theory is a conceptual class consisting of certain of these elementary statements. The elementary statements which belong to are called the elementary theorems of and said to be true. In this way, a theory is a way of designating a subset of which consists entirely of true statements.

Scientific theory

A scientific theory is a well-substantiated explanation of some aspect of the natural world that is acquired through the scientific method and repeatedly tested and confirmed through observation and experimentation. As with most (if not all) forms of scientific knowledge, scientific theories are inductive in nature and aim for predictive power and explanatory capability.

The strength of a scientific theory is related to the diversity of phenomena it can explain, and to its elegance and simplicity. See Occam's razor. As additional scientific evidence is gathered, a scientific theory may be rejected or modified if it does not fit the new empirical findings; in such circumstances, a more accurate theory is then desired. In certain cases, the less-accurate unmodified scientific theory can still be treated as a theory if it is useful (due to its sheer simplicity) as an approximation under specific conditions (e.g., Newton's laws of motion as an approximation to special relativity at velocities which are small relative to the speed of light).