Tada (disambiguation)
Tada may refer to:

TADA3L
Transcriptional adapter 3-like is a protein that in humans is encoded by the TADA3 gene.
Function
Many DNA-binding transcriptional activator proteins enhance the initiation rate of RNA polymerase II-mediated gene transcription by interacting functionally with the general transcription machinery bound at the basal promoter. Adaptor proteins are usually required for this activation, possibly to acetylate and destabilize nucleosomes, thereby relieving chromatin constraints at the promoter. The protein encoded by this gene is a transcriptional activator adaptor and has been found to be part of the PCAF histone acetylase complex. In addition, it associates with the tumor suppressor protein p53 and is required for full activity of p53 and p53-mediated apoptosis. At least four alternatively spliced variants have been found for this gene, but the full-length nature of some variants has not been determined.
Interactions
TADA3L has been shown to interact with:

Terrorist and Disruptive Activities (Prevention) Act
Terrorist and Disruptive Activities (Prevention) Act, commonly known as TADA, was an anti-terrorism law which was in force between 1985 and 1995 (modified in 1987) under the background of Punjab insurgency and was applied to whole of India. It came into effect on 23 May 1985. It was renewed in 1989, 1991 and 1993 before being allowed to lapse in 1995 due to increasing unpopularity due to widespread allegations of abuse. It was the first anti-terrorism law legislated by the government to define and counter terrorist activities.
The Act's third paragraph gives a very thorough definition of "terrorism":
Powers
The law gave wide powers to law enforcement agencies for dealing with terrorist and 'socially disruptive' activities. The police were not obliged to produce a detainee before a judicial magistrate within 24 hours. The accused person could be detained up to 1 year. Confessions made to police officers was admissible as evidence in the court of law, with the burden of proof being on the accused to prove his innocence. Courts were set up exclusively to hear the cases and deliver judgements pertaining to the persons accused under this Act. The trials could be held in camera with the identities of the witnesses kept hidden. Under 7A of the Act, Police officers were also empowered to attach the properties of the accused under this Act.
Degree
Degree may refer to:
As a unit of measurement
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field that contains the base field and satisfies additional properties. For instance, the set Q(√2) = {a + b√2 | a, b ∈ Q} is the smallest extension of Q that includes every real solution to the equation x2 = 2.
Definitions
Let L be a field. A subfield of L is a subset K of L that is closed under the field operations of L and under taking inverses in L. In other words, K is a field with respect to the field operations inherited from L. The larger field L is then said to be an extension field of K. To simplify notation and terminology, one says that L / K (read as "L over K") is a field extension to signify that L is an extension field of K.
If L is an extension of F which is in turn an extension of K, then F is said to be an intermediate field (or intermediate extension or subextension) of the field extension L / K.

Degree of a continuous mapping
In topology, the degree of a continuous mapping between two compact oriented manifolds of the same dimension is a number that represents the number of times that the domain manifold wraps around the range manifold under the mapping. The degree is always an integer, but may be positive or negative depending on the orientations.
The degree of a map was first defined by Brouwer, who showed that the degree is homotopy invariant (invariant among homotopies), and used it to prove the Brouwer fixed point theorem. In modern mathematics, the degree of a map plays an important role in topology and geometry. In physics, the degree of a continuous map (for instance a map from space to some order parameter set) is one example of a topological quantum number.
Definitions of the degree
From Sn to Sn
The simplest and most important case is the degree of a continuous map from the 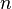 -sphere
-sphere  to itself (in the case
to itself (in the case 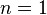 , this is called the winding number):
, this is called the winding number):
Let 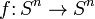 be a continuous map. Then
be a continuous map. Then 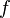 induces a homomorphism
induces a homomorphism 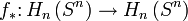 , where
, where 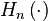 is the
is the 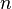 th homology group. Considering the fact that
th homology group. Considering the fact that  , we see that
, we see that 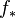 must be of the form
must be of the form 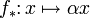 for some fixed
for some fixed 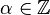 .
This
.
This 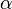 is then called the degree of
is then called the degree of 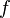 .
.
Podcasts:

