Tap (gaming)
Tapping is a term used in a variety of ways in a number of games. Although the exact meaning varies, it generally either refers to either the physical action of actually touching something, or to the "using up" of the resources of some element of the game.
Collectible card games
In collectible card games such as Magic: The Gathering to tap a card means to use it so that it cannot be used again in that player's turn. The visual indication of the tapped status is represented by turning the card 90 degrees to the right.
On cards since Revised edition (1994), tapping has been represented by a symbol, though this is not unique to the game of Magic: The Gathering. U.S. Patent 5,662,332 was filed by Wizards of the Coast to patent the mechanics of some aspects of collectible card games, including tapping.
Mechanics similar to tapping are used in many collectible card games, often involving the same 90 degree card rotation. For example, this act is referred to as setting in Ophidian 2350, while it is known as committing in the Universal Fighting System. In the medieval-Japan-themed Legend of the Five Rings, the mechanism is called "bowing". A few games, such as the City of Heroes Collectible Card Game, use several different rotational increments (90, 180, and 270 degrees), each denoting a different card status.

Tap (valve)
A tap (also spigot or faucet: see usage variations) is a valve controlling the release of a liquid or gas.
Nomenclature
British Isles
US
Types
Liquid
Water for baths, sinks and basins can be provided by separate hot and cold taps; this arrangement is common in older installations, particularly in public washrooms/lavatories and utility rooms/laundries. In kitchens and bathrooms mixer taps are commonly used. In this case, hot and cold water from the two valves is mixed before reaching the outlet, allowing the water to emerge at any temperature between that of the hot and cold water supplies. Mixer taps were invented by Thomas Campbell of Saint John, New Brunswick and patented in 1880.

TAP2
TAP2 is a gene in humans that encodes the protein Antigen peptide transporter 2.
Function
The membrane-associated protein encoded by this gene is a member of the superfamily of ATP-binding cassette (ABC) transporters. ABC proteins transport various molecules across extra- and intra-cellular membranes. ABC genes are divided into seven distinct subfamilies (ABC1, MDR/TAP, MRP, ALD, OABP, GCN20, White). This protein is a member of the MDR/TAP subfamily. Members of the MDR/TAP subfamily are involved in multidrug resistance. This gene is located 7 kb telomeric to gene family member ABCB2 (TAP1). The protein encoded by this gene is involved in antigen presentation. This protein forms a heterodimer with ABCB2 in order to transport peptides from the cytoplasm to the endoplasmic reticulum. Mutations in this gene may be associated with ankylosing spondylitis, insulin-dependent diabetes mellitus, schizophrenia, and celiac disease. Alternative splicing of this gene produces two products which differ in peptide selectivity and level of restoration of surface expression of MHC class I molecules.
Dimension (data warehouse)
A dimension is a structure that categorizes facts and measures in order to enable users to answer business questions. Commonly used dimensions are people, products, place and time.
In a data warehouse, dimensions provide structured labeling information to otherwise unordered numeric measures. The dimension is a data set composed of individual, non-overlapping data elements. The primary functions of dimensions are threefold: to provide filtering, grouping and labelling.
These functions are often described as "slice and dice". Slicing refers to filtering data. Dicing refers to grouping data. A common data warehouse example involves sales as the measure, with customer and product as dimensions. In each sale a customer buys a product. The data can be sliced by removing all customers except for a group under study, and then diced by grouping by product.
A dimensional data element is similar to a categorical variable in statistics.
Typically dimensions in a data warehouse are organized internally into one or more hierarchies. "Date" is a common dimension, with several possible hierarchies:

Dimension (song)
"Dimension" is a song by Australian hard rock band Wolfmother, featured on their 2005 debut studio album Wolfmother. Written by band members Andrew Stockdale, Chris Ross and Myles Heskett, it was released as the second single from the album in Europe (and the third single overall) on 17 April 2006, charting at number 49 on the UK Singles Chart.
Music video
Directed by The Malloys, the music video for "Dimension" was first aired in the week of 13 February 2006. Prior to this, the video was featured on the 2006 extended play (EP) Dimensions.
Critical reception
In a review of Wolfmother for Blender, writer Jonah Weiner identified "Dimension" as an example of the band "at [their] hardest", describing it as an "acid anthem".NME reviewer James Jam described the song as "a throb of gonzo metal not unlike Black Sabbath playing Motown".
Track listing
All songs written and composed by Andrew Stockdale, Chris Ross, Myles Heskett.
References
Krull dimension
In commutative algebra, the Krull dimension of a commutative ring R, named after Wolfgang Krull, is the supremum of the lengths of all chains of prime ideals. The Krull dimension need not be finite even for a Noetherian ring. More generally the Krull dimension can be defined for modules over possibly non-commutative rings as the deviation of the poset of submodules.
The Krull dimension has been introduced to provide an algebraic definition of the dimension of an algebraic variety: the dimension of the affine variety defined by an ideal I in a polynomial ring R is the Krull dimension of R/I.
A field k has Krull dimension 0; more generally, k[x1, ..., xn] has Krull dimension n. A principal ideal domain that is not a field has Krull dimension 1. A local ring has Krull dimension 0 if and only if every element of its maximal ideal is nilpotent.
Explanation
We say that a chain of prime ideals of the form
 has length n. That is, the length is the number of strict inclusions, not the number of primes; these differ by 1. We define the Krull dimension of
has length n. That is, the length is the number of strict inclusions, not the number of primes; these differ by 1. We define the Krull dimension of 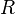 to be the supremum of the lengths of all chains of prime ideals in
to be the supremum of the lengths of all chains of prime ideals in 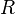 .
.
Podcasts:

