Tangent vector

In mathematics, a tangent vector is a vector that is tangent to a curve or surface at a given point. Tangent vectors are described in the differential geometry of curves in the context of curves in Rⁿ. More generally, tangent vectors are elements of a tangent space of a differentiable manifold. Tangent vectors can also be described in terms of germs. In other words, a tangent vector at the point 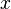is a linear derivation of the algebra defined by the set of germs at .

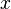Motivation

Before proceeding to a general definition of the tangent vector, we discuss its use in calculus and its tensor properties.

Calculus

Let be a parametric smooth curve. The tangent vector is given by , where we have used the a prime instead of the usual dot to indicate differentiation with respect to parameter t. the unit tangent vector is given by

Example

Given the curve

in 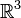, the unit tangent vector at time is given by

Contravariance

If is given parametrically in the n-dimensional coordinate system xⁱ (here we have used superscripts as an index instead of the usual subscript) by or