The English word theory was derived from a technical term in philosophy in Ancient Greek. The word theoria, θεωρία, meant "a looking at, viewing, beholding", and referring to contemplation or speculation, as opposed to action.[1] Theory is especially often contrasted to "practice" (from Greek praxis, πρᾶξις) a Greek term for "doing", which is opposed to theory because theory involved no doing apart from itself.
A classical example of the distinction between theoretical and practical uses the discipline of medicine: Medical theory and theorizing involves trying to understand the causes and nature of health and sickness, while the practical side of medicine is trying to make people healthy. These two things are related but can be independent, because it is possible to research health and sickness without curing specific patients, and it is possible to cure a patient without knowing how the cure worked.[2]
By extension of the philosophical meaning, "theoria" is also a word still used in theological contexts.
In modern contexts, while theories in the arts and philosophy may address ideas and empirical phenomena which are not easily measurable, in modern science the term "theory", or "scientific theory" is generally understood to refer to a proposed explanation of empirical phenomena, made in a way consistent with scientific method. Such theories are preferably described in such a way that any scientist in the field is in a position to understand and either provide empirical support ("verify") or empirically contradict ("falsify") it. In this modern scientific context the distinction between theory and practice corresponds roughly to the distinction between theoretical science and technology or applied science.
A common distinction made in science is between theories and hypotheses. Hypotheses are individual empirically testable conjectures; while theories are collections of hypotheses that are logically linked together into a coherent explanation of some aspect of reality and which have individually or jointly received some empirical support.
Contents |
Ancient uses [link]
Although it has more mundane meanings in Greek, the word θεωρία apparently developed special uses early in the recorded history of the Greek language. In the book From Religion to Philosophy, Francis Cornford suggests that the Orphics used the word "theory" to mean 'passionate sympathetic contemplation'.[3] Pythagoras changed the word to mean a passionate sympathetic contemplation of mathematical and scientific knowledge, because he considered such intellectual pursuits the way to reach the highest plane of existence. Pythagoras emphasized subduing emotions and bodily desires in order to enable the intellect to function at the higher plane of theory. Thus it was Pythagoras who gave the word "theory" the specific meaning which leads to the classical and modern concept of a distinction between theory as uninvolved, neutral thinking, and practice.[4]
In Aristotle's terminology, as has already been mentioned above, theory is contrasted with praxis or practice, which remains the case today. For Aristotle, both practice and theory involve thinking, but the aims are different. Theoretical contemplation considers things which humans do not move or change, such as nature, so it has no human aim apart from itself and the knowledge it helps create. On the other hand, praxis involves thinking, but always with an aim to desired actions, whereby humans cause change or movement themselves for their own ends. Any human movement which involves no conscious choice and thinking could not be an example of praxis or doing.[5]
Theories formally and scientifically [link]
Theories are analytical tools for understanding, explaining, and making predictions about a given subject matter. There are theories in many and varied fields of study, including the arts and sciences. A formal theory is syntactic in nature and is only meaningful when given a semantic component by applying it to some content (i.e. facts and relationships of the actual historical world as it is unfolding). Theories in various fields of study are expressed in natural language, but are always constructed in such a way that their general form is identical to a theory as it is expressed in the formal language of mathematical logic. Theories may be expressed mathematically, symbolically, or in common language, but are generally expected to follow principles of rational thought or logic.
Theory is constructed of a set of sentences which consist entirely of true statements about the subject matter under consideration. However, the truth of any one of these statements is always relative to the whole theory. Therefore the same statement may be true with respect to one theory, and not true with respect to another. This is, in ordinary language, where statements such as "He is a terrible person" cannot be judged to be true or false without reference to some interpretation of who "He" is and for that matter what a "terrible person" is under the theory.[6]
Sometimes two theories have exactly the same explanatory power because they make the same predictions. A pair of such theories is called indistinguishable, and the choice between them reduces to convenience or philosophical preference.
The form of theories is studied formally in mathematical logic, especially in model theory. When theories are studied in mathematics, they are usually expressed in some formal language and their statements are closed under application of certain procedures called rules of inference. A special case of this, an axiomatic theory, consists of axioms (or axiom schemata) and rules of inference. A theorem is a statement that can be derived from those axioms by application of these rules of inference. Theories used in applications are abstractions of observed phenomena and the resulting theorems provide solutions to real-world problems. Obvious examples include arithmetic (abstracting concepts of number), geometry (concepts of space), and probability (concepts of randomness and likelihood).
Gödel's incompleteness theorem shows that no consistent, recursively enumerable theory (that is, one whose theorems form a recursively enumerable set) in which the concept of natural numbers can be expressed, can include all true statements about them. As a result, some domains of knowledge cannot be formalized, accurately and completely, as mathematical theories. (Here, formalizing accurately and completely means that all true propositions—and only true propositions—are derivable within the mathematical system.) This limitation, however, in no way precludes the construction of mathematical theories that formalize large bodies of scientific knowledge.
Underdetermination [link]
A theory is underdetermined (also called indeterminacy of data to theory) if, given the available evidence cited to support the theory, there is a rival theory which is inconsistent with it that is at least as consistent with the evidence. Underdetermination is an epistemological issue about the relation of evidence to conclusions.
Intertheoretic reduction and elimination [link]
If there is a new theory which is better at explaining and predicting phenomena than an older theory (i.e. it has more explanatory power), we are justified in believing that the newer theory describes reality more correctly. This is called an intertheoretic reduction because the terms of the old theory can be reduced to the terms of the new one. For instance, our historical understanding about "sound," "light" and "heat" have today been reduced to "wave compressions and rarefactions," "electromagnetic waves," and "molecular kinetic energy," respectively. These terms which are identified with each other are called intertheoretic identities. When an old theory and a new one are parallel in this way, we can conclude that we are describing the same reality, only more completely.
In cases where a new theory uses new terms which do not reduce to terms of an older one, but rather replace them entirely because they are actually a misrepresentation it is called an intertheoretic elimination. For instance, the obsolete scientific theory that put forward an understanding of heat transfer in terms of the movement of caloric fluid was eliminated when a theory of heat as energy replaced it. Also, the theory that phlogiston is a substance released from burning and rusting material was eliminated with the new understanding of the reactivity of oxygen.
Theories vs. theorems [link]
Theories are distinct from theorems. Theorems are derived deductively from objections according to a formal system of rules, sometimes as an end in itself and sometimes as a first step in testing or applying a theory in a concrete situation; theorems are said to be true in the sense that the conclusions of a theorem are logical consequences of the objections. Theories are abstract and conceptual, and to this end they are always considered true. They are supported or challenged by observations in the world. They are 'rigorously tentative', meaning that they are proposed as true and expected to satisfy careful examination to account for the possibility of faulty inference or incorrect observation. Sometimes theories are incorrect, meaning that an explicit set of observations contradicts some fundamental objection or application of the theory, but more often theories are corrected to conform to new observations, by restricting the class of phenomena the theory applies to or changing the assertions made.
"Sometimes a hypothesis never reaches the point of being considered a theory because the answer is not found to derive its assertions analytically or not applied empirically."
Philosophical theories [link]
Theories whose subject matter consists not in empirical data, but rather in ideas are in the realm of philosophical theories as contrasted with scientific theories. At least some of the elementary theorems of a philosophical theory are statements whose truth cannot necessarily be scientifically tested through empirical observation.
Fields of study are sometimes named "theory" because their basis is some initial set of objections describing the field's approach to a subject matter. These assumptions are the elementary theorems of the particular theory, and can be thought of as the axioms of that field. Some commonly known examples include set theory and number theory; however literary theory, critical theory, and music theory are also of the same form.
Metatheory [link]
One form of philosophical theory is a metatheory or meta-theory. A metatheory is a theory whose subject matter is some other theory. In other words it is a theory about a theory. Statements made in the metatheory about the theory are called metatheorems.
Political theories [link]
A political theory is an ethical theory about the law and government. Often the term "political theory" refers to a general view, or specific ethic, political belief or attitude, about politics.
Scientific theories [link]
In scientific usage, the term "theory" is reserved for explanations of phenomena which meet basic requirements about the kinds of empirical observations made, the methods of classification used, and the consistency of the theory in its application among members of the class to which it pertains. These requirements vary across different scientific fields of knowledge, but in general theories are expected to be functional and parsimonious: i.e. a theory should be the simplest possible tool that can be used to effectively address the given class of phenomena. Such theories are constructed from elementary assumptions that are motivated by empirical data about observable phenomena. A scientific theory is used as a plausible general principle or body of principles offered to explain a phenomenon.[7]
A scientific theory is a deductive theory, in that its content is based on some formal system of logic and on basic axioms. In a deductive theory, any sentence which is a logical consequence of one or more of the axioms is also a sentence of that theory.[6]
A major concern in construction of scientific theories is the problem of demarcation, i.e., distinguishing those ideas that are properly studied by the sciences and those that are not.
Theories are intended to be an accurate, predictive description of the natural world.
Theories as models [link]
Scientific theories are constructed to explain and predict phenomena (e.g., inanimate things, events, or behavior of animals). A scientific theory can be thought of as a model of reality. According to Stephen Hawking in A Brief History of Time, "a theory is a good theory if it satisfies two requirements: It must accurately describe a large class of observations on the basis of a model which contains only a few arbitrary elements, and it must make definite predictions about the results of future observations". He goes on to state, "any physical theory is always provisional, in the sense that it is only a hypothesis; you can never prove it. No matter how many times the results of experiments agree with some theory, you can never be sure that the next time the result will not contradict the theory. On the other hand, you can disprove a theory by finding even a single observation which disagrees with the predictions of the theory". The "unprovable but falsifiable" nature of theories is a consequence of the necessity of using inductive logic.[8]
Theories in physics [link]
In physics the term theory is generally used for a mathematical framework—derived from a small set of basic postulates (usually symmetries, like equality of locations in space or in time, or identity of electrons, etc.)—which is capable of producing experimental predictions for a given category of physical systems. One good example is classical electromagnetism, which encompasses results derived from gauge symmetry (sometimes called gauge invariance) in a form of a few equations called Maxwell's equations. Note that the specific theoretical aspects of classical electromagnetic theory, which have been consistently and successfully replicated for well over a century, are termed "laws of electromagnetism", reflecting that they are today taken for granted. Within electromagnetic theory generally, there are numerous hypotheses about how electromagnetism applies to specific situations. Many of these hypotheses are already considered to be adequately tested, with new ones always in the making and perhaps untested.
Pedagogical definition [link]
In pedagogical contexts or in official pronouncements by official organizations of scientists a definition such as the following may be promulgated.
According to the United States National Academy of Sciences,
Some scientific explanations are so well established that no new evidence is likely to alter them. The explanation becomes a scientific theory. In everyday language a theory means a hunch or speculation. Not so in science. In science, the word theory refers to a comprehensive explanation of an important feature of nature supported by facts gathered over time. Theories also allow scientists to make predictions about as yet unobserved phenomena,[9]
| Look up theory in Wiktionary, the free dictionary. |
According to the American Association for the Advancement of Science,
A scientific theory is a well-substantiated explanation of some aspect of the natural world, based on a body of facts that have been repeatedly confirmed through observation and experiment. Such fact-supported theories are not "guesses" but reliable accounts of the real world. The theory of biological evolution is more than "just a theory." It is as factual an explanation of the universe as the atomic theory of matter or the germ theory of disease. Our understanding of gravity is still a work in progress. But the phenomenon of gravity, like evolution, is an accepted fact.[10]
These definitions firmly mark things termed "theories" as being well supported by evidence, although scientists sometimes also use the word "theory" to describe untested but intricate hypotheses.[citation needed]
[edit] The term theoretical
The term theoretical is sometimes informally used in place of hypothetical to describe a result that is predicted, but has not yet been adequately tested by observation or experiment. A hypothesis is a prediction which has yet to be tested, while a theory is a prediction-making conceptual framework that is consistent with data.
List of notable theories [link]
| Find more about Theory on Wikipedia's sister projects: | |
| Definitions and translations from Wiktionary |
|
| Images and media from Commons |
|
| Learning resources from Wikiversity |
|
| News stories from Wikinews |
|
| Quotations from Wikiquote |
|
| Source texts from Wikisource |
|
| Textbooks from Wikibooks |
|
- Astronomy: Big Bang Theory
- Biology: Cell theory — Evolution — Germ theory
- Chemistry: Molecular theory — Kinetic theory of gases — Molecular orbital theory — Valence bond theory — Transition state theory — RRKM theory — Chemical graph theory — Flory-Huggins solution theory — Marcus theory — Lewis theory (successor to Brønsted–Lowry acid–base theory) — HSAB theory — Debye–Hückel theory — Thermodynamic theory of polymer elasticity — Reptation theory — Polymer field theory — Møller–Plesset perturbation theory — Density Functional Theory — Frontier molecular orbital theory — Polyhedral skeletal electron pair theory — Baeyer strain theory — Quantum theory of atoms in molecules — Collision theory — Ligand field theory (successor to Crystal field theory) — Variational Transition State Theory — Benson group increment theory — Specific ion interaction theory
- Climatology: Climate change theory (due to anthropogenic activity)
- Economics: Macroeconomic theory — Microeconomic theory
- Education: Constructivist theory — Critical pedagogy theory — Education theory — Multiple intelligence theory — Progressive education theory
- Engineering: Circuit theory — Control theory — Signal theory — Systems theory — Information theory
- Film: Film Theory
- Geology: Plate tectonics
- Humanities: Critical theory
- Linguistics: X-bar theory — Government and Binding — Principles and Parameters
- Literature: Literary theory
- Mathematics: Approximation theory — Arakelov theory — Asymptotic theory — Bifurcation theory — Catastrophe theory — Category theory — Chaos theory — Choquet theory — Coding theory — Combinatorial game theory — Deformation theory — Dimension theory — Ergodic theory — Field theory — Galois theory — Game theory — Graph theory — Group theory — Hodge theory — Homology theory — Homotopy theory — Ideal theory — Intersection theory — Invariant theory — Iwasawa theory — K-theory — KK-theory — Knot theory — L-theory — Lie theory — Littlewood–Paley theory — Matrix theory — Measure theory — Model theory — Morse theory — Nevanlinna theory — Number theory — Obstruction theory — Operator theory — PCF theory — Perturbation theory — Potential theory — Probability theory — Ramsey theory — Rational choice theory — Representation theory — Ring theory — Set theory — Shape theory — Small cancellation theory — Spectral theory — Stability theory — Stable theory — Sturm–Liouville theory — Twistor theory
- Music: Music theory
- Philosophy: Proof theory — Speculative reason — Theory of truth — Type theory — Value theory — Virtue theory
- Physics: Acoustic theory — Antenna theory — Atomic theory — BCS theory — Landau theory — M-theory — Perturbation theory — Theory of relativity (successor to classical mechanics) — Quantum field theory — Scattering theory — String theory
- Planetary science: Giant impact theory
- Psychology: Cognitive dissonance theory - Attachment Theory - Object permanance - Poverty of stimulus - Attribution Theory - Self fulfilling prophecy - Stockholm syndrome
- Sociology: Sociological theory — Social theory — Critical theory
- Sports: Chess theory
- Statistics: Extreme value theory
- Theatre: Performance theory
- Visual Art: Aesthetics — Art Educational theory — Architecture — Composition — Anatomy — Color theory — Perspective — Visual perception — Geometry — Manifolds
- Other: Obsolete scientific theories — Phlogiston theory
See also [link]
Notes [link]
- ^ The word "theory" was used in Greek philosophy, for example, that of Plato. It is a statement of how and why particular facts are related. It is related to words for θεωρός "spectator", θέα thea "a view" + ὁρᾶν horan "to see", literally "looking at a show". See for example dictionary entries at Perseus website. The word has been in use in English since at least the late 16th century.Harper, Douglas. "theory". Online Etymology Dictionary. https://www.etymonline.com/index.php?term=theory. Retrieved 2008-07-18.
- ^ See for example Hippocrates Praeceptiones, Part 1.
- ^ Cornford, Francis Macdonald (November 8, 1991). From religion to philosophy: a study in the origins of western speculation. Princeton University Press. ISBN 978-0‐691‐02076‐1.
- ^ Russell, Bertrand, History of Western Philosophy
- ^ The LSJ cites two passages of Aristotle as examples, both from the Metaphysics and involving the definition of natural science: 11.1064a17, "it is clear that natural science (φυσικὴν ἐπιστήμην) must be neither practical (πρακτικὴν) nor productive (ποιητικὴν), but speculative (θεωρητικὴν)" and 6.1025b25, "Thus if every intellectual activity [διάνοια] is either practical or productive or speculative (θεωρητική), physics (φυσικὴ) will be a speculative [θεωρητική] science". So Aristotle actually made a three way distinction between practical, theoretical and productive or technical - or between doing, contemplating or making. All three types involve thinking, but are distinguished by what causes the objects of thought to move or change.
- ^ a b Curry, Haskell, Foundations of Mathematical Logic
- ^ Merriam-Webster.com Merriam-Webster Dictionary: Theory in Science
- ^ Stephen Hawking, A Brief History of Time New York: Bantam, p. 7
- ^ National Academy of Sciences (2005), Science, Evolution, and Creationism, a brochure on the book of the same title.
- ^ AAAS Evolution Resources
References [link]
- Matson, Ronald, "Comparing scientific laws and theories", Biology, Kennesaw State University, https://science.kennesaw.edu/~rmatson/3380theory.html.
- Davidson Reynolds, Paul (1971). A primer in theory construction. Boston: Allyn and Bacon.
- Hawking, Stephen (1996). "The Illustrated A Brief History of Time" (Updated and expanded ed.). New York: Bantam Books, p. 15.
- Popper, Karl (1963), Conjectures and Refutations, Routledge and Kegan Paul, London, UK, pp. 33–39. Reprinted in Theodore Schick (ed., 2000), Readings in the Philosophy of Science, Mayfield Publishing Company, Mountain View, CA, USA, pp. 9–13.
- Zima, Peter V. (2007). What is theory? Cultural theory as discourse and dialogue. London: Continuum (translated from: Was ist Theorie? Theoriebegriff und Dialogische Theorie in der Kultur- und Sozialwissenschaften. Tübingen: A. Franke Verlag, 2004).
https://wn.com/Theory

Chess theory
The game of chess is commonly divided into three phases: the opening, middlegame, and endgame. There is a large body of theory regarding how the game should be played in each of these phases, especially the opening and endgame. Those who write about chess theory, who are often but not necessarily also eminent players, are referred to as "theorists" or "theoreticians".
"Opening theory" commonly refers to consensus, broadly represented by current literature on the openings. "Endgame theory" consists of statements regarding specific positions, or positions of a similar type, though there are few universally applicable principles. "Middlegame theory" often refers to maxims or principles applicable to the middlegame. The modern trend, however, is to assign paramount importance to analysis of the specific position at hand rather than to general principles.
The development of theory in all of these areas has been assisted by the vast literature on the game. In 1913, preeminent chess historian H. J. R. Murray wrote in his 900-page magnum opus A History of Chess that, "The game possesses a literature which in contents probably exceeds that of all other games combined." He estimated that at that time the "total number of books on chess, chess magazines, and newspapers devoting space regularly to the game probably exceeds 5,000". In 1949, B. H. Wood opined that the number had increased to about 20,000.David Hooper and Kenneth Whyld wrote in 1992 that, "Since then there has been a steady increase year by year of the number of new chess publications. No one knows how many have been printed..." The world's largest chess library, the John G. White Collection at the Cleveland Public Library, contains over 32,000 chess books and serials, including over 6,000 bound volumes of chess periodicals. Chess players today also avail themselves of computer-based sources of information.
Theory (mathematical logic)
In mathematical logic, a theory (also called a formal theory) is a set of sentences in a formal language. Usually a deductive system is understood from context. An element  of a theory
of a theory 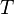 is then called an axiom of the theory, and any sentence that follows from the axioms (
is then called an axiom of the theory, and any sentence that follows from the axioms ( ) is called a theorem of the theory. Every axiom is also a theorem. A first-order theory is a set of first-order sentences.
) is called a theorem of the theory. Every axiom is also a theorem. A first-order theory is a set of first-order sentences.
Theories expressed in formal language generally
When defining theories for foundational purposes, additional care must be taken and normal set-theoretic language may not be appropriate.
The construction of a theory begins by specifying a definite non-empty conceptual class  , the elements of which are called statements. These initial statements are often called the primitive elements or elementary statements of the theory, to distinguish them from other statements which may be derived from them.
, the elements of which are called statements. These initial statements are often called the primitive elements or elementary statements of the theory, to distinguish them from other statements which may be derived from them.
A theory  is a conceptual class consisting of certain of these elementary statements. The elementary statements which belong to
is a conceptual class consisting of certain of these elementary statements. The elementary statements which belong to  are called the elementary theorems of
are called the elementary theorems of  and said to be true. In this way, a theory is a way of designating a subset of
and said to be true. In this way, a theory is a way of designating a subset of  which consists entirely of true statements.
which consists entirely of true statements.

Sunlight
Sunlight is a portion of the electromagnetic radiation given off by the Sun, in particular infrared, visible, and ultraviolet light. On Earth, sunlight is filtered through Earth's atmosphere, and is obvious as daylight when the Sun is above the horizon. When the direct solar radiation is not blocked by clouds, it is experienced as sunshine, a combination of bright light and radiant heat. When it is blocked by the clouds or reflects off other objects, it is experienced as diffused light. The World Meteorological Organization uses the term "sunshine duration" to mean the cumulative time during which an area receives direct irradiance from the Sun of at least 120 watts per square meter.
The ultraviolet radiation in sunlight has both positive and negative health effects, as it is both a principal source of vitamin D3 and a mutagen.
Summary
Researchers may record sunlight using a sunshine recorder, pyranometer, or pyrheliometer.
Sunlight takes about 8.3 minutes to reach Earth from the surface of the Sun. A photon starting at the centre of the Sun and changing direction every time it encounters a charged particle would take between 10,000 and 170,000 years to get to the surface.

Sunlight (album)
Sunlight is a June 1978 jazz-funk, fusion album by keyboardist Herbie Hancock. It features Hancock's vocals through a vocoder as well as performances by drummer Tony Williams and bassist Jaco Pastorius. This was when Hancock began heading towards a more mainstream Smooth Jazz/R&B fusion, similar to fellow Jazz-Fusion pianist Patrice Rushen. This would last until his 1982 album Lite Me Up.
The album produced a single entitled "I Thought It Was You" which was mildly received at the time by UK jazz listeners. As a whole the album tends to lay more toward funk than a jazz record, and is reminiscent of much of the electro-funk of the time. This release marks the beginning of the 1980s electro-era style that was more refined in Herbie's later albums such as Future Shock and Sound-System.
Track listing
All tracks composed by Herbie Hancock, except where indicated.
Side one

Sunlight (cleaning product)
Sunlight is a brand of household soap originally produced by the British company Lever Brothers in 1884. It was the world's first packaged, branded laundry soap. Designed for washing clothes and general household use, the success of the product led to the name for the company's village for its workers, Port Sunlight. The soap formula was invented by a Bolton chemist named William Hough Watson, who also became an early business partner. Watson's process created a new soap, using glycerin and vegetable oils such as palm oil rather than tallow (animal fats).William Lever and his brother James Darcy Lever invested in Watson's soap invention and its initial success came from offering bars of cut, wrapped, and branded soap in his father's grocery shop. Prior to this, commercially made soap was bought in long bars, an early labour-saving device for the housewife.
Sunlight was eventually supplanted by modern products made from synthetically produced detergents rather than naturally derived soaps.

