Subset

In mathematics, especially in set theory, a set A is a subset of a set B, or equivalently B is a superset of A, if A is "contained" inside B, that is, all elements of A are also elements of B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment.

The subset relation defines a partial order on sets.

The algebra of subsets forms a Boolean algebra in which the subset relation is called inclusion.

Definitions

If A and B are sets and every element of A is also an element of B, then:

A is a subset of (or is included in) B, denoted by

A \subseteq B

B is a superset of (or includes) A, denoted by

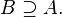
B \supseteq A.

If A is a subset of B, but A is not equal to B (i.e. there exists at least one element of B which is not an element of A), then

A is also a proper (or strict) subset of B; this is written as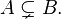

A \subsetneq B.

B is a proper superset of A; this is written as

B \supsetneq A.

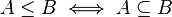For any set S, the inclusion relation ⊆ is a partial order on the set $\mathcal{P}(S)$ of all subsets of S (the power set of S) defined by $A \leq B \iff A \subseteq B$ . We may also partially order $\mathcal{P}(S)$ by reverse set inclusion by defining $A \leq B \iff B \subseteq A$ .