Scale-step
In Schenkerian theory, a scale-step (German: Stufe) is a triad (based on one of the diatonic scale degrees) that is perceived as an organizing force for a passage of music (in accordance with the principle of composing-out). In Harmony, Schenker gives the following example and asserts that
A scale-step triad is designated by an uppercase Roman numeral representing the scale degree of the root, much as in traditional "harmonic analysis" (see chord progression). Thus, in the above example (which is in G major), the G major triad that Schenker claims we perceive through the first two measures would be labelled "I". However, unlike traditional harmonic analyses, Schenker's theory is not concerned with the mere labelling of such chords, but rather with discerning hierarchical relationships among tones. For Schenker, the chords occurring in a passage need not be of equal import. As he explains:
Furthermore, in terms of Schenker's mature theory, the question of whether a given triad possesses scale-step status depends on the structural level under discussion. Indeed, it follows from Schenker's concepts that, at the highest level, a tonal composition possesses only one scale step, since the entirety of the work may be understood as an elaboration of its tonic triad (i.e. scale-step I).
Stufe (algebra)
In field theory, the Stufe (/ʃtuːfə/; German: level) s(F) of a field F is the least number of squares that sum to -1. If -1 cannot be written as a sum of squares, s(F)= . In this case, F is a formally real field. Albrecht Pfister proved that the Stufe, if finite, is always a power of 2, and that conversely every power of 2 occurs.
. In this case, F is a formally real field. Albrecht Pfister proved that the Stufe, if finite, is always a power of 2, and that conversely every power of 2 occurs.
Powers of 2
If  then
then  for some
for some  .
.
Proof: Let  be chosen such that
be chosen such that  . Let
. Let  . Then there are
. Then there are  elements
elements  such that
such that
Both  and
and 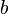 are sums of
are sums of 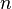 squares, and
squares, and  , since otherwise
, since otherwise  , contrary to the assumption on
, contrary to the assumption on  .
.
According to the theory of Pfister forms, the product  is itself a sum of
is itself a sum of 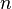 squares, that is,
squares, that is,  for some
for some  . But since
. But since  , we also have
, we also have  , and hence
, and hence
and thus  .
.
Positive characteristic
The Stufe  for all fields
for all fields  with positive characteristic.
with positive characteristic.
Proof: Let  . It suffices to prove the claim for
. It suffices to prove the claim for  .
.
If  then
then  , so
, so  .
.
If  consider the set
consider the set  of squares.
of squares.  is a subgroup of index
is a subgroup of index  in the cyclic group
in the cyclic group  with
with  elements. Thus
elements. Thus  contains exactly
contains exactly  elements, and so does
elements, and so does  .
Since
.
Since  only has
only has  elements in total,
elements in total,  and
and  cannot be disjoint, that is, there are
cannot be disjoint, that is, there are  with
with  and thus
and thus  .
.
Podcasts:

-
by Steve Howe
-
by Steve Howe
-
by Steve Howe
-
by Steve Howe
-
by Steve Howe
-
by Steve Howe
-
by Steve Howe
-
by Steve Howe
-
by Steve Howe
-
by Steve Howe
-
by Steve Howe
-
by Steve Howe
-
by Steve Howe
-
by Steve Howe
-
by Stefy
-
by Stefy
-
by Stefy
-
by Stefy
-
by Stefy
-
by Stefy
-
by Stefy
-
by Stefy
-
by Stefy
-
by Stefy
-
by Stefy
-
by Stefy
-
by Stew
Australia
by: Steve HowePlay the halls
See the stalls tonight
Open roads the like
Across the dateline change will never strike
Australia lies ahead
Australia, we head for the mainland
Clutching our gifts from the East
Only to find out
Planes and the highways
STrain the paths and the by-ways
Remain, still it's leading me
Closer to you
Australia, we're leaving you behind
Australia, we're taking the easy way out
From now on
"Come to," can't get away from ya still
"Come to, we'll take good care of ya."
Australia, you save your face while fashions slip
Australia, you're balanaced between
The powers' tightening grip
I've been to, it's a long way for ya still
