Split Lie algebra

In the mathematical field of Lie theory, a split Lie algebra is a pair where is a Lie algebra and is a splitting Cartan subalgebra, where "splitting" means that for all , is triangularizable. If a Lie algebra admits a splitting, it is called a splittable Lie algebra. Note that for reductive Lie algebras, the Cartan subalgebra is required to contain the center.

Over an algebraically closed field such as the complex numbers, all semisimple Lie algebras are splittable (indeed, not only does the Cartan subalgebra act by triangularizable matrices, but even stronger, it acts by diagonalizable ones) and all splittings are conjugate; thus split Lie algebras are of most interest for non-algebraically closed fields.

Split Lie algebras are of interest both because they formalize the split real form of a complex Lie algebra, and because split semisimple Lie algebras (more generally, split reductive Lie algebras) over any field share many properties with semisimple Lie algebras over algebraically closed fields – having essentially the same representation theory, for instance – the splitting Cartan subalgebra playing the same role as the Cartan subalgebra plays over algebraically closed fields. This is the approach followed in (Bourbaki 2005), for instance.

Lie algebra

In mathematics, a Lie algebra (/liː/, not /laɪ/) is a vector space together with a non-associative multiplication called "Lie bracket" . It was introduced to study the concept of infinitesimal transformations. Hermann Weyl introduced the term "Lie algebra" (after Sophus Lie) in the 1930s. In older texts, the name "infinitesimal group" is used.

Lie algebras are closely related to Lie groups which are groups that are also smooth manifolds, with the property that the group operations of multiplication and inversion are smooth maps. Any Lie group gives rise to a Lie algebra. Conversely, to any finite-dimensional Lie algebra over real or complex numbers, there is a corresponding connected Lie group unique up to covering (Lie's third theorem). This correspondence between Lie groups and Lie algebras allows one to study Lie groups in terms of Lie algebras.

Definitions

A Lie algebra is a vector space 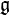over some field F together with a binary operation called the Lie bracket that satisfies the following axioms:

Lie-* algebra

In mathematics, a Lie-* algebra is a D-module with a Lie* bracket. They were introduced by Beilinson & Drinfeld (2004, section 2.5.3), and are similar to the conformal algebras discussed by Kac (1998) and to vertex Lie algebras.

References