
Silhouette
A silhouette is the image of a person, animal, object or scene represented as a solid shape of a single color, usually black, its edges matching the outline of the subject. The interior of a silhouette is featureless, and the whole is typically presented on a light background, usually white, or none at all. The silhouette differs from an outline, which depicts the edge of an object in a linear form, while a silhouette appears as a solid shape. Silhouette images may be created in any visual artistic media, but was first used to describe pieces of cut paper, which were then stuck to a backing in a contrasting colour, and often framed.
Cutting portraits, generally in profile, from black card became popular in the mid-18th century, though the term silhouette was seldom used until the early decades of the 19th century, and the tradition has continued under this name into the 21st century. They represented a cheap but effective alternative to the portrait miniature, and skilled specialist artists could cut a high-quality bust portrait, by far the most common style, in a matter of minutes, working purely by eye. Other artists, especially from about 1790, drew an outline on paper, then painted it in, which could be equally quick. The leading 18th-century English "profilist" in painting, John Miers, advertised "three minute sittings", and the cost might be as low as half a crown around 1800. Miers' superior products could be in grisaille, with delicate highlights added in gold or yellow, and some examples might be painted on various backings, including gesso, glass or ivory. The size was normally small, with many designed to fit into a locket, but otherwise a bust some 3 to 5 inches high was typical, with half- or full-length portraits proportionately larger.
Silhouettes (dance group)
The Silhouettes are a dance group from Denver, Colorado. The group is best known for performing on the sixth season of America's Got Talent. Led by Lynne (Waggoner) Patton, a choreographer from the Denver area, the 42 members of the Silhouettes range from 4-18 year olds. The group was named runner-up in the competition.
References

Silhouettes (Marmaduke Duke song)
"Silhouettes" is a song written by the Scottish experimental rock group Marmaduke Duke. It is included on their second album 'Duke Pandemonium and was released as a single on 6 July 2009. The single release of Silhouettes will be a remix version by Jacknife Lee. This version was first played by Zane Lowe on BBC Radio One in May 2009 with a preview being added to the bands Myspace page soon after.
A video has been filmed which is set to continue the story of the Duke as shown in videos for previous singles 'Kid Gloves' and 'Rubber Lover'.
References
External links
Degree
Degree may refer to:
As a unit of measurement
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field that contains the base field and satisfies additional properties. For instance, the set Q(√2) = {a + b√2 | a, b ∈ Q} is the smallest extension of Q that includes every real solution to the equation x2 = 2.
Definitions
Let L be a field. A subfield of L is a subset K of L that is closed under the field operations of L and under taking inverses in L. In other words, K is a field with respect to the field operations inherited from L. The larger field L is then said to be an extension field of K. To simplify notation and terminology, one says that L / K (read as "L over K") is a field extension to signify that L is an extension field of K.
If L is an extension of F which is in turn an extension of K, then F is said to be an intermediate field (or intermediate extension or subextension) of the field extension L / K.

Degree of a continuous mapping
In topology, the degree of a continuous mapping between two compact oriented manifolds of the same dimension is a number that represents the number of times that the domain manifold wraps around the range manifold under the mapping. The degree is always an integer, but may be positive or negative depending on the orientations.
The degree of a map was first defined by Brouwer, who showed that the degree is homotopy invariant (invariant among homotopies), and used it to prove the Brouwer fixed point theorem. In modern mathematics, the degree of a map plays an important role in topology and geometry. In physics, the degree of a continuous map (for instance a map from space to some order parameter set) is one example of a topological quantum number.
Definitions of the degree
From Sn to Sn
The simplest and most important case is the degree of a continuous map from the 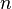 -sphere
-sphere  to itself (in the case
to itself (in the case 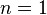 , this is called the winding number):
, this is called the winding number):
Let 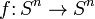 be a continuous map. Then
be a continuous map. Then 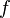 induces a homomorphism
induces a homomorphism 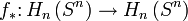 , where
, where 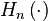 is the
is the 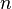 th homology group. Considering the fact that
th homology group. Considering the fact that  , we see that
, we see that 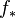 must be of the form
must be of the form 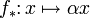 for some fixed
for some fixed 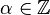 .
This
.
This 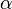 is then called the degree of
is then called the degree of 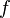 .
.
Podcasts:

