IEEE 802.1aq

Shortest Path Bridging (SPB), specified in the IEEE 802.1aq standard, is a computer networking technology intended to simplify the creation and configuration of networks, while enabling multipath routing.

It is the replacement for the older spanning tree protocols: IEEE 802.1D, IEEE 802.1w, IEEE 802.1s. These blocked any redundant paths that could result in a layer 2 loop, whereas SPB allows all paths to be active with multiple equal cost paths, provides much larger layer 2 topologies, supports faster convergence times, and improves the efficiency by allowing traffic to load share across all paths of a mesh network. It is designed to virtually eliminate human error during configuration and preserves the plug-and-play nature that established Ethernet as the de facto protocol at Layer 2.

The technology provides logical Ethernet networks on native Ethernet infrastructures using a link state protocol to advertise both topology and logical network membership. Packets are encapsulated at the edge either in media access control-in-media access control (MAC-in-MAC) 802.1ah or tagged 802.1Q/802.1ad frames and transported only to other members of the logical network. Unicast, multicast, and broadcast are supported and all routing is on a symmetric shortest paths.

This page contains text from Wikipedia, the Free Encyclopedia - https://wn.com/IEEE_802.1aq

Shortest path problem

In graph theory, the shortest path problem is the problem of finding a path between two vertices (or nodes) in a graph such that the sum of the weights of its constituent edges is minimized.

The problem of finding the shortest path between two intersections on a road map (the graph's vertices correspond to intersections and the edges correspond to road segments, each weighted by the length of its road segment) may be modeled by a special case of the shortest path problem in graphs.

Definition

The shortest path problem can be defined for graphs whether undirected, directed, or mixed. It is defined here for undirected graphs; for directed graphs the definition of path requires that consecutive vertices be connected by an appropriate directed edge.

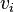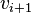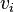Two vertices are adjacent when they are both incident to a common edge. A path in an undirected graph is a sequence of vertices $P = ( v_1, v_2, \ldots, v_n ) \in V \times V \times \ldots \times V$ such that $v_i$ is adjacent to $v_{i+1}$ for $1 \leq i < n$ . Such a path $P$ is called a path of length $n-1$ from $v_1$ to $v_n$ . (The $v_i$ are variables; their numbering here relates to their position in the sequence and needs not to relate to any canonical labeling of the vertices.)