Shodan
Shodan may refer to:

SHODAN
SHODAN (Sentient Hyper-Optimized Data Access Network) is a fictional artificial intelligence and the main antagonist of the cyberpunk-horror themed action role-playing video games System Shock and System Shock 2.
Character design
SHODAN is an artificial intelligence whose moral restraints were removed from her programming by a hacker in order for Edward Diego, station chief of Citadel Station, on which SHODAN was installed, to delete compromising files regarding illegal experiments and his corruption. She is a megalomaniac with a god complex and sees humans as little better than insects, something which she constantly reminds the player of. Her words are accompanied by stuttering, fluctuating voice pitch, shifts of timbre, and the presence of three voices speaking the same words with the constituent voices alternately lagging behind and leading ahead in different patterns, as well as computer glitches resembling a sound card malfunction. Although as a cybernetic entity SHODAN has no conventional gender, the original disc version refers to her as either an 'it' or a 'he', while the later CD version uses 'she'. On screens, SHODAN manifests herself as a green and/or grey female cybernetic face that usually wears a malevolent expression, and speaks with a chaotic, discordant voice. She is voiced by former Tribe keyboardist and vocalist, Terri Brosius, the wife of System Shock 2's sound editor, Eric Brosius, who distorted the samples to provide the distinctive SHODAN effect. In the cyberspace of System Shock, she is initially represented as an inverted blue-grey cone, reminiscent of the Master Control Program from the 1982 Disney film Tron. After she has been hacked, the cone turns red, the surface shatters and four "tentacles" or "claws" grow from the top, with her actual face starting to form above that.

Dimension (song)
"Dimension" is a song by Australian hard rock band Wolfmother, featured on their 2005 debut studio album Wolfmother. Written by band members Andrew Stockdale, Chris Ross and Myles Heskett, it was released as the second single from the album in Europe (and the third single overall) on 17 April 2006, charting at number 49 on the UK Singles Chart.
Music video
Directed by The Malloys, the music video for "Dimension" was first aired in the week of 13 February 2006. Prior to this, the video was featured on the 2006 extended play (EP) Dimensions.
Critical reception
In a review of Wolfmother for Blender, writer Jonah Weiner identified "Dimension" as an example of the band "at [their] hardest", describing it as an "acid anthem".NME reviewer James Jam described the song as "a throb of gonzo metal not unlike Black Sabbath playing Motown".
Track listing
All songs written and composed by Andrew Stockdale, Chris Ross, Myles Heskett.
References
Dimensional analysis
In engineering and science, dimensional analysis is the analysis of the relationships between different physical quantities by identifying their fundamental dimensions (such as length, mass, time, and electric charge) and units of measure (such as miles vs. kilometers, or pounds vs. kilograms vs. grams) and tracking these dimensions as calculations or comparisons are performed. Converting from one dimensional unit to another is often somewhat complex. Dimensional analysis, or more specifically the factor-label method, also known as the unit-factor method, is a widely used technique for such conversions using the rules of algebra.
The concept of physical dimension was introduced by Joseph Fourier in 1822. Physical quantities that are commensurable have the same dimension; if they have different dimensions, they are incommensurable. For example, it is meaningless to ask whether a kilogram is less, the same, or more than an hour.
Any physically meaningful equation (and likewise any inequality and inequation) will have the same dimensions on the left and right sides, a property known as "dimensional homogeneity". Checking this is a common application of dimensional analysis. Dimensional analysis is also routinely used as a check on the plausibility of derived equations and computations. It is generally used to categorize types of physical quantities and units based on their relationship to or dependence on other units.
Krull dimension
In commutative algebra, the Krull dimension of a commutative ring R, named after Wolfgang Krull, is the supremum of the lengths of all chains of prime ideals. The Krull dimension need not be finite even for a Noetherian ring. More generally the Krull dimension can be defined for modules over possibly non-commutative rings as the deviation of the poset of submodules.
The Krull dimension has been introduced to provide an algebraic definition of the dimension of an algebraic variety: the dimension of the affine variety defined by an ideal I in a polynomial ring R is the Krull dimension of R/I.
A field k has Krull dimension 0; more generally, k[x1, ..., xn] has Krull dimension n. A principal ideal domain that is not a field has Krull dimension 1. A local ring has Krull dimension 0 if and only if every element of its maximal ideal is nilpotent.
Explanation
We say that a chain of prime ideals of the form
 has length n. That is, the length is the number of strict inclusions, not the number of primes; these differ by 1. We define the Krull dimension of
has length n. That is, the length is the number of strict inclusions, not the number of primes; these differ by 1. We define the Krull dimension of 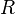 to be the supremum of the lengths of all chains of prime ideals in
to be the supremum of the lengths of all chains of prime ideals in 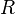 .
.
Podcasts:

