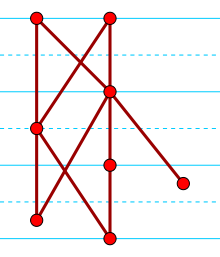
Semiorder
In order theory, a branch of mathematics, a semiorder is a type of ordering that may be determined for a set of items with numerical scores by declaring two items to be incomparable when their scores are within a given margin of error of each other, and by using the numerical comparison of their scores when those scores are sufficiently far apart. Semiorders were introduced and applied in mathematical psychology by Luce (1956) as a model of human preference without the assumption that indifference is transitive. They generalize strict weak orderings, form a special case of partial orders and interval orders, and can be characterized among the partial orders by two forbidden four-item suborders.
Definition
Let X be a set of items, and let < be a binary relation on X. Items x and y are said to be incomparable, written here as x ~ y, if neither x < y nor y < x is true. Then the pair (X,<) is a semiorder if it satisfies the following three axioms:
Podcasts:

