
Seeds (Hey Rosetta! album)
Seeds is the third studio album by Canadian indie rock band Hey Rosetta!. It was released on February 15, 2011 through Sonic Records and was produced by Tony Doogan.
Lead singer Tim Baker stated in an interview that the album name, as well as the title track, is about "...the idea is that we are seeds, traveling from town to town, blowing around, settling down here and there, trying to make something for people", and that "the songs are seeds ... they’re these little things –- four and five minute things — but they have the ability to grow in your brain and be far more meaningful than just what they are."
Reception
Seeds has received generally favorable reviews. Kate Harper of CHARTattack noted that the album "...succeeds in ways Lungs – though a good album – did not ... there's definitely more of a robust feel throughout all of Seeds." Richard Trapunski of Now Magazine gave a more mixed review: "Aiming for the same puffed-up collective catharsis as Arcade Fire, Tim Baker and co. layer strings, horns, mandolins and anything else they can get their hands on to inflate the songs into anthems."
Seeds (Agents of S.H.I.E.L.D.)
"Seeds" is the twelfth episode of the first season of the American television series Agents of S.H.I.E.L.D., based on the Marvel Comics organization S.H.I.E.L.D. (Strategic Homeland Intervention, Enforcement and Logistics Division), revolving around the character of Phil Coulson and his team of S.H.I.E.L.D. agents as they investigate attempted murder at the S.H.I.E.L.D. Science Academy. It is set in the Marvel Cinematic Universe (MCU), sharing continuity with the films of the franchise. The episode was written by Monica Owusu-Breen and Jed Whedon, and directed by Kenneth Fink.
Clark Gregg reprises his role as Coulson from the film series, and is joined by series regulars Ming-Na Wen, Brett Dalton, Chloe Bennet, Iain De Caestecker, and Elizabeth Henstridge.
"Seeds" originally aired on ABC on January 14, 2014, and according to Nielsen Media Research, was watched by 6.37 million viewers.
Plot
While at a S.H.I.E.L.D. Academy Ward, Fitz, Simmons, and Skye investigate an attack upon Seth, a popular cadet, with an "ice machine" that can freeze people and their surroundings. Another ice machine soon freezes cadet Donnie Gill, though the agents are able to save him. While the rest of the team interrogates the other cadets, Fitz befriends Donnie, seeing much of himself in him, and helps him solve a problem with a new power source. Meanwhile, Coulson and May go to Mexico City to find a former agent named Richard Lumley, who tells them of a mission 24 years earlier involving Skye, an 0-8-4 with apparent superhuman abilities. The team deduces that the cadets are building a bigger ice machine for Quinn, and with the better power source, Seth and Donnie give Quinn a demonstration, creating a massive ice storm. Though the team apprehends Donnie, Seth is killed by the storm, and Donnie gains apparent cryokinetic abilities. Later, Coulson calls Quinn, who has connections to the Clairvoyant.

Dimension (song)
"Dimension" is a song by Australian hard rock band Wolfmother, featured on their 2005 debut studio album Wolfmother. Written by band members Andrew Stockdale, Chris Ross and Myles Heskett, it was released as the second single from the album in Europe (and the third single overall) on 17 April 2006, charting at number 49 on the UK Singles Chart.
Music video
Directed by The Malloys, the music video for "Dimension" was first aired in the week of 13 February 2006. Prior to this, the video was featured on the 2006 extended play (EP) Dimensions.
Critical reception
In a review of Wolfmother for Blender, writer Jonah Weiner identified "Dimension" as an example of the band "at [their] hardest", describing it as an "acid anthem".NME reviewer James Jam described the song as "a throb of gonzo metal not unlike Black Sabbath playing Motown".
Track listing
All songs written and composed by Andrew Stockdale, Chris Ross, Myles Heskett.
References
Dimensional analysis
In engineering and science, dimensional analysis is the analysis of the relationships between different physical quantities by identifying their fundamental dimensions (such as length, mass, time, and electric charge) and units of measure (such as miles vs. kilometers, or pounds vs. kilograms vs. grams) and tracking these dimensions as calculations or comparisons are performed. Converting from one dimensional unit to another is often somewhat complex. Dimensional analysis, or more specifically the factor-label method, also known as the unit-factor method, is a widely used technique for such conversions using the rules of algebra.
The concept of physical dimension was introduced by Joseph Fourier in 1822. Physical quantities that are commensurable have the same dimension; if they have different dimensions, they are incommensurable. For example, it is meaningless to ask whether a kilogram is less, the same, or more than an hour.
Any physically meaningful equation (and likewise any inequality and inequation) will have the same dimensions on the left and right sides, a property known as "dimensional homogeneity". Checking this is a common application of dimensional analysis. Dimensional analysis is also routinely used as a check on the plausibility of derived equations and computations. It is generally used to categorize types of physical quantities and units based on their relationship to or dependence on other units.
Krull dimension
In commutative algebra, the Krull dimension of a commutative ring R, named after Wolfgang Krull, is the supremum of the lengths of all chains of prime ideals. The Krull dimension need not be finite even for a Noetherian ring. More generally the Krull dimension can be defined for modules over possibly non-commutative rings as the deviation of the poset of submodules.
The Krull dimension has been introduced to provide an algebraic definition of the dimension of an algebraic variety: the dimension of the affine variety defined by an ideal I in a polynomial ring R is the Krull dimension of R/I.
A field k has Krull dimension 0; more generally, k[x1, ..., xn] has Krull dimension n. A principal ideal domain that is not a field has Krull dimension 1. A local ring has Krull dimension 0 if and only if every element of its maximal ideal is nilpotent.
Explanation
We say that a chain of prime ideals of the form
 has length n. That is, the length is the number of strict inclusions, not the number of primes; these differ by 1. We define the Krull dimension of
has length n. That is, the length is the number of strict inclusions, not the number of primes; these differ by 1. We define the Krull dimension of 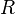 to be the supremum of the lengths of all chains of prime ideals in
to be the supremum of the lengths of all chains of prime ideals in 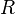 .
.
Podcasts:

