Modular group

In mathematics, the modular group is the projective special linear group PSL(2,Z) of 2 x 2 matrices with integer coefficients and unit determinant. The matrices A and -A are identified. The modular group acts on the upper-half of the complex plane by fractional linear transformations, and the name "modular group" comes from the relation to moduli spaces and not from modular arithmetic.

Definition

The modular group Γ is the group of linear fractional transformations of the upper half of the complex plane which have the form

where a, b, c, and d are integers, and ad − bc = 1. The group operation is function composition.

This group of transformations is isomorphic to the projective special linear group PSL(2, Z), which is the quotient of the 2-dimensional special linear group SL(2, Z) over the integers by its center {I, −I}. In other words, PSL(2, Z) consists of all matrices

where a, b, c, and d are integers, ad − bc = 1, and pairs of matrices A and −A are considered to be identical. The group operation is the usual multiplication of matrices.

Special linear Lie algebra

In mathematics, the special linear Lie algebra of order n (denoted ) is the Lie algebra of matrices with trace zero and with the Lie bracket . This algebra is well studied and understood, and is often used as a model for the study of other Lie algebras. The Lie group that it generates is the special linear group.

Applications

The Lie algebra is central to the study of special relativity, general relativity and supersymmetry: its fundamental representation is the so-called spinor representation, while its adjoint representation generates the Lorentz group SO(3,1) of special relativity.

The algebra plays an important role in the study of chaos and fractals, as it generates the Möbius group SL(2,R), which describes the automorphisms of the hyperbolic plane, the simplest Riemann surface of negative curvature; by contrast, SL(2,C) describes the automorphisms of the hyperbolic 3-dimensional ball.

Representation Theory of

The simplest non-trivial Lie algebra is , consisting of two by two matrices with zero trace. There are three basis elements, ,,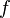 and , with