
Tikhonov regularization
Tikhonov regularization, named for Andrey Tikhonov, is the most commonly used method of regularization of ill-posed problems. In statistics, the method is known as ridge regression, and with multiple independent discoveries, it is also variously known as the Tikhonov–Miller method, the Phillips–Twomey method, the constrained linear inversion method, and the method of linear regularization. It is related to the Levenberg–Marquardt algorithm for non-linear least-squares problems.
Suppose a vector  must be found such that
must be found such that
When the problem is not well posed (either because of non-existence or non-uniqueness of 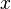 ) then the standard approach (known as ordinary least squares) leads to an overdetermined (over-fitted), or more often an underdetermined (under-fitted) system of equations. Most real-world phenomena have the effect of low-pass filters in the forward direction where
) then the standard approach (known as ordinary least squares) leads to an overdetermined (over-fitted), or more often an underdetermined (under-fitted) system of equations. Most real-world phenomena have the effect of low-pass filters in the forward direction where 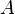 maps
maps  to
to  . Therefore in solving the inverse-problem, the inverse mapping operates as a high-pass filter that has the undesirable tendency of amplifying noise (eigenvalues / singular values are largest in the reverse mapping where they were smallest in the forward mapping). In addition, ordinary least squares implicitly nullifies every element of the reconstructed version of
. Therefore in solving the inverse-problem, the inverse mapping operates as a high-pass filter that has the undesirable tendency of amplifying noise (eigenvalues / singular values are largest in the reverse mapping where they were smallest in the forward mapping). In addition, ordinary least squares implicitly nullifies every element of the reconstructed version of  that is in the null-space of
that is in the null-space of 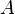 , rather than allowing for a model to be used as a prior for
, rather than allowing for a model to be used as a prior for  . Ordinary least squares seeks to minimize the sum of squared residuals, which can be compactly written as
. Ordinary least squares seeks to minimize the sum of squared residuals, which can be compactly written as


 must be found such that
must be found such that 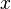 ) then the standard approach (known as
) then the standard approach (known as 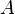 maps
maps  . Therefore in solving the inverse-problem, the inverse mapping operates as a
. Therefore in solving the inverse-problem, the inverse mapping operates as a 