¿¡Revolución!?
¿¡Revolución!? is a 2006 political documentary directed by Quebec journalist and filmmaker Charles Gervais. It examines the Bolivarian Revolution led by Venezuelan President Hugo Chávez. It was produced by Télé-Québec, the Quebec government's public television network.
As part of the Rencontres internationales du documentaire de Montréal film festival, first screenings occurred on November 10 and 14, 2006 at the Cinéma ONF in Montreal. The general opening happened on December 8, 2006, at Cinéma Ex-Centris, also in Montreal. This version showed the original Spanish spoken by the subjects, as well as narration and subtitles in French.
Production
In April 2005, director Charles Gervais heard of the news that Hugo Chávez decided to distribute one million free copies of major 17th century Spanish novel Don Quixote de la Mancha to Venezuelan citizens. This gave him the inspiration to fly to Venezuela and examine from within this "revolution" in the making. Also, after filming the medium-length documentary Quand la vie est un rêve on the Haitian youth, Gervais wished to focus on something more positive.
Revolution (B-Boy Anthem)
"Revolution (B-Boy Anthem)" is a single by Oakland Hip Hop group Zion I, released in 2000 through Ground Control Records. "Revolution" was the opening track and the lead single for the group's debut album Mind Over Matter, and also spawned the group's first music video. The single features two remixes of the song, the "Armageddon Mix" and the "Dirty Dirty Mix".
Track listing
A-Side
B-Side
External links
Revolution (cycling series)
Revolution is a series of track cycling events primarily held at the Manchester Velodrome in the north west of England. It was solely held in Manchester between 2003 and 2012. From Season 10 (2012-2013) meetings have been held additionally at the new UK velodromes; in the Sir Chris Hoy Velodrome, Glasgow, the Olympic Velodrome, London from Season 11 (2013-2014) and the Derby Arena from 2015-16.
The series comprises four or five meetings each year, held between October and February, on Saturday evenings. The series showcases various top cyclists, both British and other international riders, regularly attracting a large number of spectators. The recent success of the British team, including Chris Hoy's triple Gold at the 2008 Summer Olympics and double Gold winning performance at the 2012 Summer Olympics has meant that the events now regularly sell out in advance.
Concept
The series was founded in 2003, with the main aim of providing regular track cycling events for fans to attend in Manchester. Previously, track cycling fans were generally only able to attend one international event in Manchester each year, usually a round of the UCI Track Cycling World Cup Classics series, or as in 2000, the UCI Track Cycling World Championships. The only other events held regularly at the velodrome were events such as the British National Track Championships, which have a lower profile and therefore attracted smaller crowds.
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field that contains the base field and satisfies additional properties. For instance, the set Q(√2) = {a + b√2 | a, b ∈ Q} is the smallest extension of Q that includes every real solution to the equation x2 = 2.
Definitions
Let L be a field. A subfield of L is a subset K of L that is closed under the field operations of L and under taking inverses in L. In other words, K is a field with respect to the field operations inherited from L. The larger field L is then said to be an extension field of K. To simplify notation and terminology, one says that L / K (read as "L over K") is a field extension to signify that L is an extension field of K.
If L is an extension of F which is in turn an extension of K, then F is said to be an intermediate field (or intermediate extension or subextension) of the field extension L / K.
Degree (graph theory)
In graph theory, the degree (or valency) of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex 
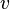is denoted 
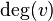or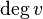 
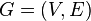. The maximum degree of a graph G, denoted by Δ(G), and the minimum degree of a graph, denoted by δ(G), are the maximum and minimum degree of its vertices. In the graph on the right, the maximum degree is 5 and the minimum degree is 0. In a regular graph, all degrees are the same, and so we can speak of the degree of the graph.
Handshaking lemma
The degree sum formula states that, given a graph 
,
The formula implies that in any graph, the number of vertices with odd degree is even. This statement (as well as the degree sum formula) is known as the handshaking lemma. The latter name comes from a popular mathematical problem, to prove that in any group of people the number of people who have shaken hands with an odd number of other people from the group is even.
Degree sequence
The degree sequence of an undirected graph is the non-increasing sequence of its vertex degrees; for the above graph it is (5, 3, 3, 2, 2, 1, 0). The degree sequence is a graph invariant so isomorphic graphs have the same degree sequence. However, the degree sequence does not, in general, uniquely identify a graph; in some cases, non-isomorphic graphs have the same degree sequence.
Podcasts:
