Circular sector

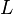A circular sector or circle sector (symbol: ⌔), is the portion of a disk enclosed by two radii and an arc, where the smaller area is known as the minor sector and the larger being the major sector. In the diagram, θ is the central angle in radians, the radius of the circle, and is the arc length of the minor sector.

A sector with the central angle of 180° is called a half-disk and is bounded by a diameter and a semicircle. Sectors with other central angles are sometimes given special names, these include quadrants (90°), sextants (60°) and octants (45°), which come from the sector being one 4th or 6th or 8th part of a full circle, respectively.

The angle formed by connecting the endpoints of the arc to any point on the circumference that is not in the sector is equal to half the central angle.

Area

The total area of a circle is . The area of the sector can be obtained by multiplying the circle's area by the ratio of the angle and (because the area of the sector is proportional to the its angle, and is the angle for the whole circle, in radians):

Quadrant (plane geometry)

The axes of a two-dimensional Cartesian system divide the plane into four infinite regions, called quadrants, each bounded by two half-axes.

These are often numbered from 1st to 4th and denoted by Roman numerals: I (where the signs of the two coordinates are (+,+)), II (−,+), III (−,−), and IV (+,−). When the axes are drawn according to the mathematical custom, the numbering goes counter-clockwise starting from the upper right ("northeast") quadrant.

See also

External links

Cartesian coordinate system

A Cartesian coordinate system is a coordinate system that specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular directed lines, measured in the same unit of length. Each reference line is called a coordinate axis or just axis of the system, and the point where they meet is its origin, usually at ordered pair (0, 0). The coordinates can also be defined as the positions of the perpendicular projections of the point onto the two axes, expressed as signed distances from the origin.

One can use the same principle to specify the position of any point in three-dimensional space by three Cartesian coordinates, its signed distances to three mutually perpendicular planes (or, equivalently, by its perpendicular projection onto three mutually perpendicular lines). In general, n Cartesian coordinates (an element of real n-space) specify the point in an n-dimensional Euclidean space for any dimension n. These coordinates are equal, up to sign, to distances from the point to n mutually perpendicular hyperplanes.

Galactic quadrant

A galactic quadrant, or quadrant of the Galaxy, refers to one of four circular sectors in the division of the Milky Way Galaxy.

Quadrants in the galactic coordinate system

In actual astronomical practice, the delineation of the galactic quadrants is based upon the galactic coordinate system, which places the Sun as the pole of the mapping system. The Sun is used instead of the Galactic Center for practical reasons since all astronomical observations (by humans) to date have been based on Earth or within the solar system.

Delineation

Quadrants are described using ordinals—for example, "1st galactic quadrant" "second galactic quadrant," or "third quadrant of the Galaxy." Viewing from the north galactic pole with 0 degrees (°) as the ray that runs starting from the Sun and through the galactic center, the quadrants are as follow:

Circle

A circle is a simple shape in Euclidean geometry. It is the set of all points in a plane that are at a given distance from a given point, the centre; equivalently it is the curve traced out by a point that moves so that its distance from a given point is constant. The distance between any of the points and the centre is called the radius.

A circle is a simple closed curve which divides the plane into two regions: an interior and an exterior. In everyday use, the term "circle" may be used interchangeably to refer to either the boundary of the figure, or to the whole figure including its interior; in strict technical usage, the circle is only the boundary and the whole figure is called a disk.

A circle may also be defined as a special ellipse in which the two foci are coincident and the eccentricity is 0, or the two-dimensional shape enclosing the most area per unit perimeter squared, using calculus of variations.

Terminology

Circle (2014 film)

Circle (Turkish: Daire) is a 2014 film written and directed by director Atil Inac.

Plot

In the hard-boiled world, where will the soft-shelled end up? A cozy kind of extermination is on the stage and keeping a low profile. The decadence around us is nothing less than clandestine annihilation of the civil man. Yet it is carried out so well with a grinning face, it is officially sold as transition. Now that the tamed indulgent is striped off social justice, welfare, even denied the tender love of concentration camps and slavery plantations of past centuries. At least hand them a round of rope… They have high expectations from taking things in their own hands.

Circle is a peculiar story of an ordinary man caught between an untimely romance and brave new hostile world.

Characters

Awards

Circle (Eddie Izzard)

Circle is the name of a stand-up tour by the comedian Eddie Izzard in 2000.

It was released on VHS and DVD in the United Kingdom on 18 November 2002. The video includes Eddie performing a French version of his show with English subtitles.

The performance features many of Izzard's traditional themes, particularly religion (or "philosophies with some good ideas, and some fucking weird ones"). A discussion about Jesus' role in the three main Abrahamic faiths sees him "waiting offstage" in Judaism and playing on the same sporting team as Muhammad in Islam. This is counterpointed with a dialogue between a Crusader and his enemy in which both men are trying to kill the other "in the name of Jesus". He also mentions his impression that in Buddhism, Jesus is "Buddha's baby brother Benny".

The rigidity of religion is also lampooned, particularly as it relates to the Renaissance. Galileo's persecution by the Catholic Church is mentioned, although the man is eventually asked (in prison) "Galileo, Galileo, will you do the fandango?"