Prandtl–Glauert transformation
The Prandtl–Glauert transformation is a mathematical technique which allows solving certain compressible flow problems by incompressible-flow calculation methods. It also allows applying incompressible-flow data to compressible-flow cases.
Mathematical formulation
Inviscid compressible flow over slender bodies is governed by linearized compressible small-disturbance potential equation:
together with the small-disturbance flow-tangency boundary condition.
is the freestream Mach number, and 
are the surface-normal vector components. The unknown variable is the perturbation potential 
, and the total velocity is given by its gradient plus the freestream velocity 
which is assumed here to be along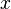 
.
The above formulation is valid only if the small-disturbance approximation applies ,
and in addition that there is no transonic flow, approximately stated by the requirement that the local Mach number not exceed unity.
![\left[1 + (\gamma+1) \frac{\phi_x}{V_\infty} \right] M_\infty^2 \;<\; 1](http://assets.wn.com/wiki/en/9/f6/5f39eb05bac66a48eb2ed-8126a5.png)
The Prandtl-Glauert (PG) transformation uses the Prandtl-Glauert Factor
. It consists of scaling down all y and z dimensions and angle of attack by the factor of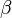 
, and the potential by 
.
Podcasts:
