
Conclusion (music)
In music, the conclusion is the ending of a composition and may take the form of a coda or outro.
Pieces using sonata form typically use the recapitulation to conclude a piece, providing closure through the repetition of thematic material from the exposition in the tonic key. In all musical forms other techniques include "altogether unexpected digressions just as a work is drawing to its close, followed by a return...to a consequently more emphatic confirmation of the structural relations implied in the body of the work."
For example:

Psyence Fiction
Psyence Fiction is the debut album by the group Unkle, released in 1998 for Mo'Wax.
Notes
"Unreal" is an instrumental version of the song "Be There" (featuring Ian Brown), which was released a year later as a single. On some early presses of the album, instrumental versions of "Guns Blazing" and "The Knock" were added as tracks 13 and 14. On some re-releases of this album, "Be There" was added as track 13. Some versions (mainly the Japanese release, but also the US promotional copy) contain the hidden track "Intro (optional)" as "track zero", which is actually the pre-gap (index 0) of track 1. This can be accessed by "rewinding" the first track on some CD players.
"Lonely Soul" was featured in an Assassin's Creed trailer for PS3, Xbox 360, and PC. It was also featured on the soundtrack to the film The Beach, in the first episode of Misfits and in the Person of Interest episode "Matsya Nyaya".
Psyence Fiction reached #4 on the UK album charts, and #107 on US Billboard 200. It also debuted at #15 in Australia.

Closing credits
Closing credits or end credits are added at the very ending of a motion picture, television program, or video game to list the cast and crew involved in the production. They usually appear as a list of names in small type, which either flip very quickly from page to page, or move smoothly across the background or a black screen. Credits may crawl either right-to-left (which is common in U.K. and some Latin American television programs) or bottom-to-top (which is common in films and U.S. television). The term credit roll comes from the early production days when the names were literally printed on a roll of paper and wound past the camera lens. Sometimes, post-credits scenes or bloopers are added to the end of films along with the closing credits.
History
The use of closing credits in film to list complete production crew and cast was not firmly established in American film until the 1970s. Before this decade, most movies were released with no closing credits at all. Films generally had opening credits only, which consisted of just major cast and crew, although sometimes the names of the cast and the characters they played would be shown at the end, as in The Wizard of Oz, Citizen Kane, Mary Poppins, Oliver! and the 1964 Fail Safe. Two of the first major films to contain extensive closing credits – but almost no opening credits – were the blockbusters Around the World in 80 Days (1956) and West Side Story (1961). West Side Story showed only the title at the beginning of the film, and Around the World in 80 Days, like many films today, had no opening credits at all.

Dimension (song)
"Dimension" is a song by Australian hard rock band Wolfmother, featured on their 2005 debut studio album Wolfmother. Written by band members Andrew Stockdale, Chris Ross and Myles Heskett, it was released as the second single from the album in Europe (and the third single overall) on 17 April 2006, charting at number 49 on the UK Singles Chart.
Music video
Directed by The Malloys, the music video for "Dimension" was first aired in the week of 13 February 2006. Prior to this, the video was featured on the 2006 extended play (EP) Dimensions.
Critical reception
In a review of Wolfmother for Blender, writer Jonah Weiner identified "Dimension" as an example of the band "at [their] hardest", describing it as an "acid anthem".NME reviewer James Jam described the song as "a throb of gonzo metal not unlike Black Sabbath playing Motown".
Track listing
All songs written and composed by Andrew Stockdale, Chris Ross, Myles Heskett.
References
Dimensional analysis
In engineering and science, dimensional analysis is the analysis of the relationships between different physical quantities by identifying their fundamental dimensions (such as length, mass, time, and electric charge) and units of measure (such as miles vs. kilometers, or pounds vs. kilograms vs. grams) and tracking these dimensions as calculations or comparisons are performed. Converting from one dimensional unit to another is often somewhat complex. Dimensional analysis, or more specifically the factor-label method, also known as the unit-factor method, is a widely used technique for such conversions using the rules of algebra.
The concept of physical dimension was introduced by Joseph Fourier in 1822. Physical quantities that are commensurable have the same dimension; if they have different dimensions, they are incommensurable. For example, it is meaningless to ask whether a kilogram is less, the same, or more than an hour.
Any physically meaningful equation (and likewise any inequality and inequation) will have the same dimensions on the left and right sides, a property known as "dimensional homogeneity". Checking this is a common application of dimensional analysis. Dimensional analysis is also routinely used as a check on the plausibility of derived equations and computations. It is generally used to categorize types of physical quantities and units based on their relationship to or dependence on other units.
Krull dimension
In commutative algebra, the Krull dimension of a commutative ring R, named after Wolfgang Krull, is the supremum of the lengths of all chains of prime ideals. The Krull dimension need not be finite even for a Noetherian ring. More generally the Krull dimension can be defined for modules over possibly non-commutative rings as the deviation of the poset of submodules.
The Krull dimension has been introduced to provide an algebraic definition of the dimension of an algebraic variety: the dimension of the affine variety defined by an ideal I in a polynomial ring R is the Krull dimension of R/I.
A field k has Krull dimension 0; more generally, k[x1, ..., xn] has Krull dimension n. A principal ideal domain that is not a field has Krull dimension 1. A local ring has Krull dimension 0 if and only if every element of its maximal ideal is nilpotent.
Explanation
We say that a chain of prime ideals of the form
 has length n. That is, the length is the number of strict inclusions, not the number of primes; these differ by 1. We define the Krull dimension of
has length n. That is, the length is the number of strict inclusions, not the number of primes; these differ by 1. We define the Krull dimension of 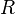 to be the supremum of the lengths of all chains of prime ideals in
to be the supremum of the lengths of all chains of prime ideals in 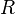 .
.
Podcasts:

