Multinomial test
In statistics, the multinomial test is the test of the null hypothesis that the parameters of a multinomial distribution equal specified values. It is used for categorical data; see Read and Cressie.
We begin with a sample of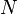 
items each of which has been observed to fall into one of 
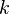categories. We can define 
as the observed numbers of items in each cell. Hence 
.
Next, we define a vector of parameters 
, where :
. These are the parameter values under the null hypothesis.
The exact probability of the observed configuration 
under the null hypothesis is given by
The significance probability for the test is the probability of occurrence of the data set observed, or of a data set less likely than that observed, if the null hypothesis is true. Using an exact test, this is calculated as
where the sum ranges over all outcomes as likely as, or less likely than, that observed. In practice this becomes computationally onerous as 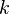and 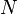increase so it is probably only worth using exact tests for small samples. For larger samples, asymptotic approximations are accurate enough and easier to calculate.
Podcasts:
