Multilinear map
In linear algebra, a multilinear map is a function of several variables that is linear separately in each variable. More precisely, a multilinear map is a function
where 
and 
are vector spaces (or modules over a commutative ring), with the following property: for each 
, if all of the variables but 
are held constant, then 
is a linear function of .
A multilinear map of one variable is a linear map, and of two variables is a bilinear map. More generally, a multilinear map of k variables is called a k-linear map. If the codomain of a multilinear map is the field of scalars, it is called a multilinear form. Multilinear maps and multilinear forms are fundamental objects of study in multilinear algebra.
If all variables belong to the same space, one can consider symmetric, antisymmetric and alternating k-linear maps. The latter coincide if the underlying ring (or field) has a characteristic different from two, else the former two coincide.
Examples
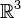.Podcasts:
