Mean value analysis
In queueing theory, a discipline within the mathematical theory of probability, mean value analysis (MVA) is a recursive technique for computing expected queue lengths, waiting time at queueing nodes and throughput in equilibrium for a closed separable system of queues. The first approximate techniques were published independently by Schweitzer and Bard, followed later by an exact version by Lavenberg and Reiser published in 1980.
It is based on the arrival theorem, which states that when one customer in an M-customer closed system arrives at a service facility he/she observes the rest of the system to be in the equilibrium state for a system with M − 1 customers.
Problem setup
Consider a closed queueing network of K M/M/1 queues, with M customers circulating in the system. To compute the mean queue length and waiting time at each of the nodes and throughput of the system we use an iterative algorithm starting with a network with 0 customers.
Write μi for the service rate at node i and P for the customer routing matrix where element pij denotes the probability that a customer finishing service at node i moves to node j for service. To use the algorithm we first compute the visit ratio row vector v, a vector such that v = v P.
Value engineering
Value engineering (VE) is systematic method to improve the "value" of goods or products and services by using an examination of function. Value, as defined, is the ratio of function to cost. Value can therefore be increased by either improving the function or reducing the cost. It is a primary tenet of value engineering that basic functions be preserved and not be reduced as a consequence of pursuing value improvements.
The reasoning behind value engineering is as follows: if marketers expect a product to become practically or stylistically obsolete within a specific length of time, they can design it to only last for that specific lifetime. The products could be built with higher-grade components, but with value-engineering they are not because this would impose an unnecessary cost on the manufacturer, and to a limited extent also an increased cost on the purchaser. Value engineering will reduce these costs. A company will typically use the least expensive components that satisfy the product's lifetime projections.

Mean
In mathematics, mean has several different definitions depending on the context.
In probability and statistics, mean and expected value are used synonymously to refer to one measure of the central tendency either of a probability distribution or of the random variable characterized by that distribution. In the case of a discrete probability distribution of a random variable X, the mean is equal to the sum over every possible value weighted by the probability of that value; that is, it is computed by taking the product of each possible value x of X and its probability P(x), and then adding all these products together, giving 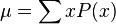 . An analogous formula applies to the case of a continuous probability distribution. Not every probability distribution has a defined mean; see the Cauchy distribution for an example. Moreover, for some distributions the mean is infinite: for example, when the probability of the value
. An analogous formula applies to the case of a continuous probability distribution. Not every probability distribution has a defined mean; see the Cauchy distribution for an example. Moreover, for some distributions the mean is infinite: for example, when the probability of the value  is
is 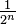 for n = 1, 2, 3, ....
for n = 1, 2, 3, ....
For a data set, the terms arithmetic mean, mathematical expectation, and sometimes average are used synonymously to refer to a central value of a discrete set of numbers: specifically, the sum of the values divided by the number of values. The arithmetic mean of a set of numbers x1, x2, ..., xn is typically denoted by  , pronounced "x bar". If the data set were based on a series of observations obtained by sampling from a statistical population, the arithmetic mean is termed the sample mean (denoted
, pronounced "x bar". If the data set were based on a series of observations obtained by sampling from a statistical population, the arithmetic mean is termed the sample mean (denoted  ) to distinguish it from the population mean (denoted
) to distinguish it from the population mean (denoted 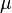 or
or 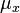 ).
).
Podcasts:

