Maximum flow problem

In optimization theory, maximum flow problems involve finding a feasible flow through a single-source, single-sink flow network that is maximum.

The maximum flow problem can be seen as a special case of more complex network flow problems, such as the circulation problem. The maximum value of an s-t flow (i.e., flow from source s to sink t) is equal to the minimum capacity of an s-t cut (i.e., cut severing s from t) in the network, as stated in the max-flow min-cut theorem.

History

The maximum flow problem was first formulated in 1954 by T. E. Harris and F. S. Ross as a simplified model of Soviet railway traffic flow. In 1955, Lester R. Ford, Jr. and Delbert R. Fulkerson created the first known algorithm, the Ford–Fulkerson algorithm.

Over the years, various improved solutions to the maximum flow problem were discovered, notably the shortest augmenting path algorithm of Edmonds and Karp and independently Dinitz; the blocking flow algorithm of Dinitz; the push-relabel algorithm of Goldberg and Tarjan; and the binary blocking flow algorithm of Goldberg and Rao. The electrical flow algorithm of Christiano, Kelner, Madry, and Spielman finds an approximately optimal maximum flow but only works in undirected graphs.

Flow network

In graph theory, a flow network (also known as a transportation network) is a directed graph where each edge has a capacity and each edge receives a flow. The amount of flow on an edge cannot exceed the capacity of the edge. Often in operations research, a directed graph is called a network. The vertices are called nodes and the edges are called arcs. A flow must satisfy the restriction that the amount of flow into a node equals the amount of flow out of it, unless it is a source, which has only outgoing flow, or sink, which has only incoming flow. A network can be used to model traffic in a road system, circulation with demands, fluids in pipes, currents in an electrical circuit, or anything similar in which something travels through a network of nodes.

Definition

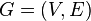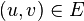Let be a finite directed graph in which every edge has a non-negative, real-valued capacity 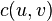. If 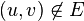, we assume that 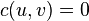. We distinguish two vertices: a source s and a sink t. A flow in a flow network is a real function 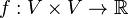with the following three properties for all nodes u and v: