SNP (complexity)
In computational complexity theory, SNP (from Strict NP) is a complexity class containing a limited subset of NP based on its logical characterization in terms of graph-theoretical properties. It forms the basis for the definition of the class MaxSNP of optimization problems.
One characterization of the NP complexity class, as shown by Ronald Fagin in 1974 and related to Fagin's theorem, is that it is the set of problems that can be reduced to properties of graphs expressible in existential second-order logic. This logic allows universal (∀) and existential (∃) quantification over vertices, but only existential quantification over sets of vertices and relations between vertices. SNP retains existential quantification over sets and relations, but only permits universal quantification over vertices.
SNP contains k-SAT, the boolean satisfiability problem (SAT) where the formula is restricted to conjunctive normal form and to at most k literals per clause, where k is fixed.
MaxSNP
APX
In complexity theory the class APX (an abbreviation of "approximable") is the set of NP optimization problems that allow polynomial-time approximation algorithms with approximation ratio bounded by a constant (or constant-factor approximation algorithms for short). In simple terms, problems in this class have efficient algorithms that can find an answer within some fixed multiplicative factor of the optimal answer.
An approximation algorithm is called a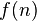 
-approximation algorithm for input size 
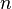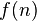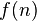if it can be proven that the solution that the algorithm finds is at most a multiplicative factor of times worse than the optimal solution. Here, is called the approximation ratio. Problems in APX are those with algorithms for which the approximation ratio is a constant 
. The approximation ratio is conventionally stated greater than 1. In the case of minimization problems, 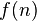is the found solution's score divided by the optimum solution's score, while for maximization problems the reverse is the case. For maximization problems, where an inferior solution has a smaller score, 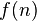is sometimes stated as less than 1; in such cases, the reciprocal of 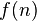is the ratio of the score of the found solution to the score of the optimum solution.
Podcasts:
