Lumina
Lumina may refer to:

LUMINA
LUMINA, also known as 201 Folsom Street, is a 655-unit residential development project under construction in the Rincon Hill neighborhood of San Francisco. Developed by Tishman Speyer, it is located one block to the southwest of its sister project, The Infinity.
History
The project was originally approved in September 2003 concurrently with its sister project, The Infinity. Tishman Speyer developed The Infinity first, completing it in 2009. Meanwhile, 201 Folsom Street was left unbuilt, and with its permits set to expire, Tishman Speyer was granted a three year extension in 2009. After being redesigned by Arquitectonica, another 12-month extension was granted in 2012.
In February 2013, Tishman Speyer announced that it had formed a joint venture with China Vanke to develop 201 Folsom Street. According to Reuters, China Vanke agreed to contribute $175 million for a 70% stake, and Tishman Speyer $75 million for a 30% stake. The remainder of the project's $620 million cost was to be financed with debt. Tishman Speyer received its building permits in May 2013 and construction commenced in June.

Dimension (song)
"Dimension" is a song by Australian hard rock band Wolfmother, featured on their 2005 debut studio album Wolfmother. Written by band members Andrew Stockdale, Chris Ross and Myles Heskett, it was released as the second single from the album in Europe (and the third single overall) on 17 April 2006, charting at number 49 on the UK Singles Chart.
Music video
Directed by The Malloys, the music video for "Dimension" was first aired in the week of 13 February 2006. Prior to this, the video was featured on the 2006 extended play (EP) Dimensions.
Critical reception
In a review of Wolfmother for Blender, writer Jonah Weiner identified "Dimension" as an example of the band "at [their] hardest", describing it as an "acid anthem".NME reviewer James Jam described the song as "a throb of gonzo metal not unlike Black Sabbath playing Motown".
Track listing
All songs written and composed by Andrew Stockdale, Chris Ross, Myles Heskett.
References
Dimensional analysis
In engineering and science, dimensional analysis is the analysis of the relationships between different physical quantities by identifying their fundamental dimensions (such as length, mass, time, and electric charge) and units of measure (such as miles vs. kilometers, or pounds vs. kilograms vs. grams) and tracking these dimensions as calculations or comparisons are performed. Converting from one dimensional unit to another is often somewhat complex. Dimensional analysis, or more specifically the factor-label method, also known as the unit-factor method, is a widely used technique for such conversions using the rules of algebra.
The concept of physical dimension was introduced by Joseph Fourier in 1822. Physical quantities that are commensurable have the same dimension; if they have different dimensions, they are incommensurable. For example, it is meaningless to ask whether a kilogram is less, the same, or more than an hour.
Any physically meaningful equation (and likewise any inequality and inequation) will have the same dimensions on the left and right sides, a property known as "dimensional homogeneity". Checking this is a common application of dimensional analysis. Dimensional analysis is also routinely used as a check on the plausibility of derived equations and computations. It is generally used to categorize types of physical quantities and units based on their relationship to or dependence on other units.
Krull dimension
In commutative algebra, the Krull dimension of a commutative ring R, named after Wolfgang Krull, is the supremum of the lengths of all chains of prime ideals. The Krull dimension need not be finite even for a Noetherian ring. More generally the Krull dimension can be defined for modules over possibly non-commutative rings as the deviation of the poset of submodules.
The Krull dimension has been introduced to provide an algebraic definition of the dimension of an algebraic variety: the dimension of the affine variety defined by an ideal I in a polynomial ring R is the Krull dimension of R/I.
A field k has Krull dimension 0; more generally, k[x1, ..., xn] has Krull dimension n. A principal ideal domain that is not a field has Krull dimension 1. A local ring has Krull dimension 0 if and only if every element of its maximal ideal is nilpotent.
Explanation
We say that a chain of prime ideals of the form
 has length n. That is, the length is the number of strict inclusions, not the number of primes; these differ by 1. We define the Krull dimension of
has length n. That is, the length is the number of strict inclusions, not the number of primes; these differ by 1. We define the Krull dimension of 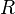 to be the supremum of the lengths of all chains of prime ideals in
to be the supremum of the lengths of all chains of prime ideals in 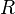 .
.
Podcasts:

