Latest News for: lower numbering
Edit
Zelensky wants more weapons before lowering conscription age
Beijing News 15 Jan 2025
Zelensky's comments come amid growing pressure from Kiev's sponsors, particularly the United States, to lower Ukraine's conscription age to 18 to bolster troop numbers ... number occurring in 2024 alone.
Edit
 The Hawk Eye
15 Jan 2025
The Hawk Eye
15 Jan 2025
'We create a safety net': Fort Madison Fire Department releases their 2024 report
 The Hawk Eye
15 Jan 2025
The Hawk Eye
15 Jan 2025
The total number of emergency response calls the fire department responded to was lower in 2024 than it was the previous two years, with the department responding to 1,693 emergency calls (compared to 1,714 in 2022 and 1,820 in 2023).
Edit
Sleazy Does It: Decius Interviewed
The Quietus 15 Jan 2025
Questions were asked with the eyes and the hands, because merely by being there, everyone had a secret ... II – Splendour & Obedience), is made by men who identify with the lower – i.e. straighter – numbers on The Kinsey Scale ... Vol ... Saoudi interjects.
Edit
Dow Jones DIA ETF is falling: 3 catalysts that could end the crash
Invezz 14 Jan 2025
Therefore, the DIA ETF needs these numbers to come lower than expected since that would change the view about the Fed and lower the rising bond yields ... Netflix, GE Aviation, Johnson & Johnson, and Verizon will also report their numbers next week.
Edit
 Beaumont Enterprise
14 Jan 2025
Beaumont Enterprise
14 Jan 2025
Georgia cuts loose more people from probation after a fitful start
 Beaumont Enterprise
14 Jan 2025
Beaumont Enterprise
14 Jan 2025
The state with the highest per capita number of people on probation is trying to lower that number.
Edit
Irregular migration into the European Union fell sharply last year, border agency says
Newsday 14 Jan 2025
The agency said that there were just over 239,000 detections of irregular border crossings, the lowest number registered since 2021, when migration was lower due to the COVID-19 pandemic.
Edit
'Game Changer' box office collection day 4: The Ram Charan starrer slows down on first Monday, expected to cross Rs 100 crore on Makar Sankranti
The Times of India 14 Jan 2025
Edit
3 children now dead after Lower Sackville house fire
CBC 14 Jan 2025
According to an online fundraiser for the family, two more children have died following a duplex fire early Saturday morning in Lower Sackville, N.S., bringing the number of fatalities to three ... .
Edit
Tragic Crocodile Attack Claims Young Girl’s Life in Indonesia
Watan 14 Jan 2025
Since 2014, at least 478 people have been killed and 531 others injured in crocodile attacks, although these figures are believed to be lower than the actual numbers. Agencies ....
Edit
GOP senator shamed for decrying standards in Dept. of Defense while misspelling 'military'
Raw Story 14 Jan 2025
Edit
Religious attendance linked to slower cognitive decline in Hispanic older adults
PsyPost 14 Jan 2025- 1
- 2
- Next page »

 of a finite
of a finite 
 for the valuation, the ring of integers and its maximal ideal for
for the valuation, the ring of integers and its maximal ideal for 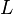 . As a consequence of
. As a consequence of ![\mathcal O_L = \mathcal O_K[\alpha]](http://assets.wn.com/wiki/en/3/17/a981b4a66d1de2605fd5c-5c1900.png) for some
for some  where
where 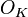 is the ring of integers of
is the ring of integers of 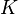 . (This is stronger than the
. (This is stronger than the  , we define
, we define 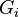 to be the set of all
to be the set of all 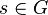 that satisfies the following equivalent conditions.
that satisfies the following equivalent conditions. operates trivially on
operates trivially on 
 for all
for all 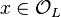
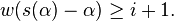
 -th ramification group. They form a decreasing
-th ramification group. They form a decreasing  the
the  the wild inertia subgroup of
the wild inertia subgroup of  is called the tame quotient.
is called the tame quotient.