Krull dimension
In commutative algebra, the Krull dimension of a commutative ring R, named after Wolfgang Krull, is the supremum of the lengths of all chains of prime ideals. The Krull dimension need not be finite even for a Noetherian ring. More generally the Krull dimension can be defined for modules over possibly non-commutative rings as the deviation of the poset of submodules.
The Krull dimension has been introduced to provide an algebraic definition of the dimension of an algebraic variety: the dimension of the affine variety defined by an ideal I in a polynomial ring R is the Krull dimension of R/I.
A field k has Krull dimension 0; more generally, k[x1, ..., xn] has Krull dimension n. A principal ideal domain that is not a field has Krull dimension 1. A local ring has Krull dimension 0 if and only if every element of its maximal ideal is nilpotent.
Explanation
We say that a chain of prime ideals of the form
has length n. That is, the length is the number of strict inclusions, not the number of primes; these differ by 1. We define the Krull dimension of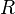 
to be the supremum of the lengths of all chains of prime ideals in .
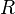