Please tell us which country and city you'd like to see the weather in.

Jordan normal form
In linear algebra, a Jordan normal form (often called Jordan canonical form) of a linear operator on a finite-dimensional vector space is an upper triangular matrix of a particular form called a Jordan matrix, representing the operator with respect to some basis. Such a matrix has each non-zero off-diagonal entry equal to 1, immediately above the main diagonal (on the superdiagonal), and with identical diagonal entries to the left and below them.
If the vector space is over a field K, then a basis with respect to which the matrix has the required form exists if and only if all eigenvalues of the matrix lie in K, or equivalently if the characteristic polynomial of the operator splits into linear factors over K. This condition is always satisfied if K is the field of complex numbers. The diagonal entries of the normal form are the eigenvalues (of the operator), and the number of times each eigenvalue occurs is called the algebraic multiplicity of the eigenvalue.
If the operator is originally given by a square matrix M, then its Jordan normal form is also called the Jordan normal form of M. Any square matrix has a Jordan normal form if the field of coefficients is extended to one containing all the eigenvalues of the matrix. In spite of its name, the normal form for a given M is not entirely unique, as it is a block diagonal matrix formed of Jordan blocks, the order of which is not fixed; it is conventional to group blocks for the same eigenvalue together, but no ordering is imposed among the eigenvalues, nor among the blocks for a given eigenvalue, although the latter could for instance be ordered by weakly decreasing size.
Normal form
Normal form may refer to:
In formal language theory:
In logic:
In lambda calculus:
See also

Set (music)
A set (pitch set, pitch-class set, set class, set form, set genus, pitch collection) in music theory, as in mathematics and general parlance, is a collection of objects. In musical contexts the term is traditionally applied most often to collections of pitches or pitch-classes, but theorists have extended its use to other types of musical entities, so that one may speak of sets of durations or timbres, for example.
A set by itself does not necessarily possess any additional structure, such as an ordering. Nevertheless, it is often musically important to consider sets that are equipped with an order relation (called segments); in such contexts, bare sets are often referred to as "unordered", for the sake of emphasis.
Two-element sets are called dyads, three-element sets trichords (occasionally "triads", though this is easily confused with the traditional meaning of the word triad). Sets of higher cardinalities are called tetrachords (or tetrads), pentachords (or pentads), hexachords (or hexads), heptachords (heptads or, sometimes, mixing Latin and Greek roots, "septachords"—e.g.,), octachords (octads), nonachords (nonads), decachords (decads), undecachords, and, finally, the dodecachord.
Normal form (bifurcation theory)
In mathematics, the normal form of a bifurcation is a simple dynamical system which is equivalent to all systems exhibiting this bifurcation.
Normal forms are defined for local bifurcations. It is assumed that the system is first reduced to the center manifold of the equilibrium point at which the bifurcation takes place. The reduced system is then locally (around the equilibrium) topologically equivalent to the normal form of the bifurcation.
For example, the normal form of a saddle-node bifurcation is  where
where 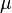 is the bifurcation parameter.
is the bifurcation parameter.
References

Jordan Village, Connecticut
Jordan is a village in the town of Waterford, Connecticut, and the historic center of the town. It was named from the Jordan River. The village was listed on the National Register of Historic Places as Jordan Village Historic District in 1990. The district includes 58 contributing buildings and one other contributing site over an area of 57 acres (23 ha). It includes examples of Greek Revival and Queen Anne architectural styles.
Location
Jordan Village is located on land known historically as Jordan Plain, a flat land area at the head of Jordan Cove, an estuary off Long Island Sound. The historic district surrounds the intersection of Rope Ferry Road and North Road.
See also
References

Jordan (Bishop of Poland)
Jordan (died in 982 or 984) was the first Bishop of Poland from 968 with his seat, most probably, in Poznań. He was an Italian or German.
Most evidence shows that he was missionary bishop subordinate directly to the Pope. He arrived in Poland, probably from Italy or the Rhineland, in 966 with Doubravka of Bohemia to baptise Mieszko I of Poland. After the death of Jordan until 992 the throne of the Bishop of Poland was vacant, or there was a bishop of unknown name (the first theory is more probable). His successor, from 992, was Unger.
References

Jordan 198
The Jordan 198 was the car with which the Jordan Formula One team used to compete in the 1998 Formula One season. It was driven by 1996 World Champion Damon Hill, who had moved from Arrows, and Ralf Schumacher, who was in his second season with the team.
After a dismal start which saw the team fail to score a single championship point in the first half of the season, numerous improvements to the car and tyre development by Goodyear enabled Jordan to climb back into the top teams. At the 1998 Belgian Grand Prix, the team scored a historic first victory with Hill, with Schumacher finishing behind him in second place. The team finished fourth in the Constructors' Championship, one ahead of Benetton.
Complete Formula One results
(key) (results in bold indicate pole position)
References
Radio Stations - Amman
| RADIO STATION | GENRE | LOCATION |
|---|---|---|
| Mazaj 95.3 FM | World Middle East | Jordan |
| Beat FM (JO) | Pop | Jordan |
| Sawt el Ghad Amman | World Middle East | Jordan |
| Halimiat | World Middle East | Jordan |
SEARCH FOR RADIOS
Podcasts:
Jordan
ALBUMS
- Use Your Ears Vol. 3 released: 2012
- Super Eurobeat, Volume 197: King of Eurobeat released: 2009
- Tunnel Trance Force, Volume 48 released: 2009
- Summer Trance, Volume 1 released: 2007
- Dance Max 2007.01 released: 2007
- Dancefloor 2008 released: 2007
- Dream Dance 43 released: 2007
Use Your Ears Vol. 3
Released 2012- When The Sun Goes Down
- Houze Thiz
- VSJ
- Flashbob
- Hold You
- Just Remember
- We Started Dancing
- Love You More
- The Whisperer
- The Same Thing
- Left, Left
- Rescue Me
- Truth Hurts
- A Priori (Noir Remix)
- Feel Me (Mario Basanov Remix)
- Remember (Inxec Vs. Droog Remix)
- Lonely Days (Hunter/Game Remix)
- About You (Fur Coat Remix)
- Villains (Daniel Dexter Remix)
- Found Out (Deetron Sunshower Remix)
Super Eurobeat, Volume 197: King of Eurobeat
Released 2009- Super Eurobeat
- Don't Turn It Off
- The Champion
- Love Countdown
- Fire Dragon
- I Was Born for Burning
- In the Flame of Fire
- Dancing in the Starlight
- Fly Away
- Bad Tonight
- Thank You - Arigato
- Bad Illusion
- Roppongi Nights
- Highway Star
- Heroes
- Sledge Hammer
- Doctor of Love
- Music Fever
- Take Me Now
- Touch Me Baby
- Fool for Your Loving
- Like a Space Invader (Saturday version)
- I'm Alive
- King of the Race
- A Flash in the Night
- Don't Let Me Go
- Loved in Tokyo
- Ivanhoe
- I Feel Like a Molotov
- King of Eurobeat
Tunnel Trance Force, Volume 48
Released 2009- Tricky Tricky 2009 (Jens O. club remix)
- The Darkside (DJ Gollum remix)
- Suck My Dick (DJ Selecta Tanzflächen rework)
- The One 2009 (Instumental mix) (feat. Dee Dee)
- Numb (RainDropz! mix)
- Funky Beatzz (Full Grainer remix)
- This Beat Is What You Need (DJDean remix)
- In the Shadows (Tunnel Allstars DJ Team remix)
- The Energy (Deepforces remix)
- I Can't Stop Raving (original mix)
- Going Nowhere (DJ Fait remix)
- Tears Don't Lie (Dream Dance Alliance remix)
- Nie Wieder (club mix)
- See the Light 2009
- Super Crazy (Discotronic remix)
- Evolution (club mix)
- Sexy Vampire (DJ Fire remix edit)
- When I Listen to Music (extended mix)
- On Y Va (Tube Tonic & DJ Shandar remix)
- I Feel You (Soulcry & Gainworx remix)
- Paradise (Megastylez remix)
- Umamama (Megastylez remix)
- Believe in Future (DJ Lanai remix)
- Ignition
- Come On (short mix)
- All Yours
Summer Trance, Volume 1
Released 2007- Komodo (DDA radio mix)
- Dreamworld
- Your Love
- Tonight (dub radio mix)
- Jordan Is Back
- Close Horizon (Guiseppe Ottaviani radio mix)
- When Love Becomes a Lie (Cascada radio mix)
- Forever
- Don't Stop Till You Get Enough (Pakito radio mix)
- Now Is the Time
- Feel (DJ Shog remix edit)
- Why?
- Full Moon
- Loosing Sences (vocal radio mix)
- Universe Inside
- Hold Me Till the End (Ronski Speed radio mix)
- Good for Me
- Smile
- Why Don't You Talk About Me
- Call the Galaxy Taxi
Dance Max 2007.01
Released 2007- Your Love
- The Silmarilla 2007
- Pulverturm 2.0
- 4Ever
- Jordan Is Back
- Fucking Beautiful
- Let It Go
- If I Were You
- Sunshine
- Check This!
- Behind the Cow
- Where Are You 2007
- Eye of the Tiger
- Flight 643 (Ricard Dwad remix)
- Time After Time
- The Final
- This Is My Sound (Hear It & Love It) (vocal club edit)
- Rock the House
- Yeah Yeah
- The Beat Is Rockin'
Dancefloor 2008
Released 2007- Children
- Everybody Clap Yo Hands (feat. Joe Bataan) (Mondo edit)
- Ride Like the Wind
- Mr. Pink
- Ready or Not
- I Dream
- Medicine (Topmodelz radio mix)
- Virgin of Love (Rave Allstars edit)
- Divided
- Gone
- Front Attack (Bass Up! radio mix)
- Check This Out
- Gar I Seng Med Laren
- Love Is All Over
- Waiting (Cobbi edit)
- Destiny
- Each Time You Break My Heart 2007 (Cuba club radio edit)
- Lets Go Out Tonight (feat. TK) (Burnett & Cooper radio mix)
- Ghostbusters
- Keep On
Dream Dance 43
Released 2007- Lethal Industry (Richard Durand remix edit)
- Analog Feel
- Close Horizon (Giuseppe Ottaviani remix edit)
- A Life Elsewhere (Martin Roth remix edit)
- Light at the End (Lost World remix edit)
- Helix
- Insolation (Ferry Corsten remix edit)
- Good for Me
- Duality
- Beautiful People
- Sleepwalking (Duderstadt remix edit)
- Ankh - Breath of Life
- Celebrate the Light (Rene Ablaze radio mix)
- Devinded
- The Chosen
- Hope
- Back in the Sun (Saint Rush radio edit)
- Leave Behind
- Magenta
- Afterlite
Jordan
ALBUMS
- Hablando con el universo released: 2011
- La pura percepción released: 2007
Jordan
ALBUMS
- alma&perfil released: 2009
- Focus 360º released: 2007
alma&perfil
Released 2009- Intro
- 1,86 Do Céu
- Palavras A Mais
- Alma&Perfil
- Blue Instrumental
- Dizem Que Não Há Saida
- Espero Que O Azar Me Esqueça
- Instrumental ''esquecimento''
- Última Rimas
- Qualquercoisa E Um Pouco Dejazz
- Naquele Hotel
- Se Este Amor Fosse Errado
- Ponto De Fuga (Got To Move On)
- Instrumental ''sem Ressentimentos''
- Fico Como Sou
- E Porque Nao
- Digo-Vos A Verdade (Como Feitiço)
Jordan
ALBUMS
Jordan
ALBUMS

