Join (SQL)
A SQL join clause combines records from two or more tables in a relational database. It creates a set that can be saved as a table or used as it is. A JOIN is a means for combining fields from two tables (or more) by using values common to each. ANSI-standard SQL specifies five types of JOIN: INNER, LEFT OUTER, RIGHT OUTER, FULL OUTER and CROSS. As a special case, a table (base table, view, or joined table) can JOIN to itself in a self-join.
A programmer writes a JOIN statement to identify records for joining. If the evaluated predicate is true, the combined record is then produced in the expected format, a record set or a temporary table.
Sample tables
Relational databases are usually normalized to eliminate duplication of information such as when objects have one-to-many relationships. For example, a Department may be associated with a number of Employees. Joining separate tables for Department and Employee effectively creates another table which combines the information from both tables. This is at some expense in terms of the time it takes to compute the join. While it is also possible to simply maintain a denormalized table if speed is important, duplicate information may take extra space, and add the expense and complexity of maintaining data integrity if data which is duplicated later changes.

SQL
SQL (![]() i/ˈɛs kjuː ˈɛl/, or
i/ˈɛs kjuː ˈɛl/, or ![]() i/ˈsiːkwəl/;Structured Query Language) is a special-purpose programming language designed for managing data held in a relational database management system (RDBMS), or for stream processing in a relational data stream management system (RDSMS).
i/ˈsiːkwəl/;Structured Query Language) is a special-purpose programming language designed for managing data held in a relational database management system (RDBMS), or for stream processing in a relational data stream management system (RDSMS).
Originally based upon relational algebra and tuple relational calculus, SQL consists of a data definition language, data manipulation language, and a data control language. The scope of SQL includes data insert, query, update and delete, schema creation and modification, and data access control. Although SQL is often described as, and to a great extent is, a declarative language (4GL), it also includes procedural elements.
SQL was one of the first commercial languages for Edgar F. Codd's relational model, as described in his influential 1970 paper, "A Relational Model of Data for Large Shared Data Banks." Despite not entirely adhering to the relational model as described by Codd, it became the most widely used database language.
SQL 2008
SQL 2008 can refer to
SQL-92
SQL-92 was the third revision of the SQL database query language. Unlike SQL-89, it was a major revision of the standard. For all but a few minor incompatibilities, the SQL-89 standard is forward compatible with SQL-92.
The standard specification itself grew about five times compared to SQL-89. Much of it was due more precise specifications of existing features; the increase due to new features was only by a factor of 1.5–2. Many of the new features had already been implemented by vendors before the new standard was adopted. However, most of the new features were added to the "intermediate" and "full" tiers of the specification, meaning that conformance with SQL-92 entry level was scarcely any more demanding than conformance with SQL-89.
Later revisions of the standard include SQL:1999 (SQL3), SQL:2003, SQL:2008, and SQL:2011.
New features
Significant new features include:
DATE, TIME, TIMESTAMP, INTERVAL, BIT string, VARCHAR strings, and NATIONAL CHARACTER strings.Join
Join may refer to:
- Join (mathematics), a least upper bound of set orders in lattice theory
- Join (topology), an operation combining two topological spaces
- Join (relational algebra), a type of binary operator
- Join (sigma algebra), a refinement of sigma algebras

Lattice (order)
In mathematics, a lattice is one of the fundamental algebraic structures used in abstract algebra. It consists of a partially ordered set in which every two elements have a unique supremum (also called a least upper bound or join) and a unique infimum (also called a greatest lower bound or meet). An example is given by the natural numbers, partially ordered by divisibility, for which the unique supremum is the least common multiple and the unique infimum is the greatest common divisor.
Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities. Since the two definitions are equivalent, lattice theory draws on both order theory and universal algebra. Semilattices include lattices, which in turn include Heyting and Boolean algebras. These "lattice-like" structures all admit order-theoretic as well as algebraic descriptions.
Lattices as partially ordered sets
If (L, ≤) is a partially ordered set (poset), and S⊆L is an arbitrary subset, then an element u∈L is said to be an upper bound of S if s≤u for each s∈S. A set may have many upper bounds, or none at all. An upper bound u of S is said to be its least upper bound, or join, or supremum, if u≤x for each upper bound x of S. A set need not have a least upper bound, but it cannot have more than one. Dually, l∈L is said to be a lower bound of S if l≤s for each s∈S. A lower bound l of S is said to be its greatest lower bound, or meet, or infimum, if x≤l for each lower bound x of S. A set may have many lower bounds, or none at all, but can have at most one greatest lower bound.

Join (topology)
In topology, a field of mathematics, the join of two topological spaces A and B, often denoted by  , is defined to be the quotient space
, is defined to be the quotient space
where I is the interval [0, 1] and R is the equivalence relation generated by
At the endpoints, this collapses  to
to 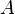 and
and  to
to  .
.
Intuitively,  is formed by taking the disjoint union of the two spaces and attaching a line segment joining every point in A to every point in B.
is formed by taking the disjoint union of the two spaces and attaching a line segment joining every point in A to every point in B.
Properties
is homeomorphic to the reduced suspension
of the smash product. Consequently, since  is contractible, there is a homotopy equivalence
is contractible, there is a homotopy equivalence
Examples
Podcasts:

