| Look up inverse in Wiktionary, the free dictionary. |
|
Inverse may refer to:
- Inverse (logic), a type of immediate inference from a conditional sentence
- Inverse (program), a program for solving inverse and optimization problems
- Inverse multiplexer (or 'demultiplexer'), which breaks a single data stream into several streams with lower data rates
- "Invert", a term used in the exotic pet industry to refer to arthropods
- Inversions (novel), a science fiction novel by Iain M. Banks
Science, engineering and mathematics [link]
- Inverse (mathematics)
- Inversive geometry, transformation geometry based on inversion in a circle
- Inverse problem, in science and mathematics, fitting a model to known data
- Multiplicative inverse, a set of numbers which when multiplied yield the multiplicative identity, 1
- Invert, the bottom of a sewer or tunnel, particularly if masonry lined. It may be flat or form a continuous curve with the tunnel arch.
See also [link]
- Inversion (disambiguation)
- Inverter (disambiguation)
- Opposite (disambiguation)
- Reverse (disambiguation)
| This disambiguation page lists articles associated with the same title. If an internal link led you here, you may wish to change the link to point directly to the intended article. |
https://wn.com/Inverse
Inverse (mathematics)
In many contexts in mathematics the term inverse indicates the opposite of something. This word and its derivatives are used widely in mathematics, as illustrated below.
- the additive inverse of x is −x;
- the multiplicative inverse or reciprocal of x is x−1.
- inverse function — inverse element with respect to function composition: a function that "reverses" the action of a given function: f−1(f(x)) = x.
Inverse element
In abstract algebra, the idea of an inverse element generalises concepts of a negation (sign reversal) in relation to addition, and a reciprocal in relation to multiplication. The intuition is of an element that can 'undo' the effect of combination with another given element. While the precise definition of an inverse element varies depending on the algebraic structure involved, these definitions coincide in a group.
The word 'inverse' is derived from Latin: inversus that means 'turned upside down', 'overturned'.
Formal definitions
In a unital magma
Let  be a set with a binary operation
be a set with a binary operation  (i.e., a
(i.e., a magma note that a magma also has closure under the binary operation). If  is an identity element of
is an identity element of  (i.e., S is a unital magma) and
(i.e., S is a unital magma) and  , then
, then  is called a left inverse of
is called a left inverse of 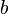 and
and 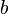 is called a right inverse of
is called a right inverse of  . If an element
. If an element 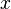 is both a left inverse and a right inverse of
is both a left inverse and a right inverse of  , then
, then 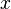 is called a two-sided inverse, or simply an inverse, of
is called a two-sided inverse, or simply an inverse, of  . An element with a two-sided inverse in
. An element with a two-sided inverse in  is called invertible in
is called invertible in  . An element with an inverse element only on one side is left invertible, resp. right invertible. A unital magma in which all elements are invertible is called a loop. A loop whose binary operation satisfies the associative law is a group.
. An element with an inverse element only on one side is left invertible, resp. right invertible. A unital magma in which all elements are invertible is called a loop. A loop whose binary operation satisfies the associative law is a group.

