Directed graph

In mathematics, and more specifically in graph theory, a directed graph (or digraph) is a graph, or set of vertices connected by edges, where the edges have a direction associated with them. In formal terms, a directed graph is an ordered pair G = (V, A) (sometimes G = (V, E)) where

It differs from an ordinary or undirected graph, in that the latter is defined in terms of unordered pairs of vertices, which are usually called edges, arcs, or lines.

A directed graph is called a simple digraph if it has no multiple arrows (two or more edges that connect the same two vertices in the same direction) and no loops (edges that connect vertices to themselves). A directed graph is called a directed multigraph or multidigraph if it may have multiple arrows (and sometimes loops). In the latter case the arrow set forms a multiset, rather than a set, of ordered pairs of vertices.

Degree (graph theory)

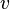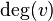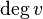In graph theory, the degree (or valency) of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex is denoted or . The maximum degree of a graph G, denoted by Δ(G), and the minimum degree of a graph, denoted by δ(G), are the maximum and minimum degree of its vertices. In the graph on the right, the maximum degree is 5 and the minimum degree is 0. In a regular graph, all degrees are the same, and so we can speak of the degree of the graph.

Handshaking lemma

The degree sum formula states that, given a graph ,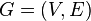

The formula implies that in any graph, the number of vertices with odd degree is even. This statement (as well as the degree sum formula) is known as the handshaking lemma. The latter name comes from a popular mathematical problem, to prove that in any group of people the number of people who have shaken hands with an odd number of other people from the group is even.

Degree sequence

The degree sequence of an undirected graph is the non-increasing sequence of its vertex degrees; for the above graph it is (5, 3, 3, 2, 2, 1, 0). The degree sequence is a graph invariant so isomorphic graphs have the same degree sequence. However, the degree sequence does not, in general, uniquely identify a graph; in some cases, non-isomorphic graphs have the same degree sequence.