Iliad
The Iliad (/ˈɪliəd/;Ancient Greek: Ἰλιάς Ilias, pronounced [iː.li.ás] in Classical Attic; sometimes referred to as the Song of Ilion or Song of Ilium) is an ancient Greek epic poem in dactylic hexameter, traditionally attributed to Homer. Set during the Trojan War, the ten-year siege of the city of Troy (Ilium) by a coalition of Greek states, it tells of the battles and events during the weeks of a quarrel between King Agamemnon and the warrior Achilles.
Although the story covers only a few weeks in the final year of the war, the Iliad mentions or alludes to many of the Greek legends about the siege; the earlier events, such as the gathering of warriors for the siege, the cause of the war, and related concerns tend to appear near the beginning. Then the epic narrative takes up events prophesied for the future, such as Achilles' looming death and the sack of Troy, prefigured and alluded to more and more vividly, so that when it reaches an end, the poem has told a more or less complete tale of the Trojan War.
Ilias (disambiguation)
Ilias Greek: Ηλίας is the Greek version of the name of the Prophet Elijah.
Persons with Ilias as given name
Ribbon (mathematics)
In mathematics (differential geometry) by a ribbon (or strip) 
is meant a smooth space curve 
given by a three-dimensional vector 
, depending continuously on the curve arc-length 
(
), together with a smoothly varying unit vector 
perpendicular to at each point (Blaschke 1950).
The ribbon is called simple and closed if is simple (i.e. without self-intersections) and closed and if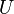 
and all its derivatives agree at 
and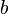 
.
For any simple closed ribbon the curves 
given parametrically by 
are, for all sufficiently small positive 
, simple closed curves disjoint from .
The ribbon concept plays an important role in the Cǎlugǎreǎnu-White-Fuller formula (Fuller 1971), that states that
where 
is the asymptotic (Gauss) linking number (a topological quantity), 
denotes the total writhing number (or simply writhe) and 
is the total twist number (or simply twist).
Ribbon theory investigates geometric and topological aspects of a mathematical reference ribbon associated with physical and biological properties, such as those arising in topological fluid dynamics, DNA modeling and in material science.
Ribbon (company)
Ribbon is a San Francisco payments startup that lets users sell online using a shortened URL that can be shared across email, social media and a seller's own website. The service focuses on bring integrated checkouts directly to platforms like Facebook, YouTube, and Twitter letting buyers purchase without leaving those services.
The company graduated from a startup accelerator called AngelPad as "Kout" in October 2011 and subsequently raised $1.6 million from Tim Draper through Draper Associates, Naguib Sawiris, Emil Michael, Gokul Rajaram, and others bringing its total raised amount to $1.75 million.
Twitter shutdown
On April 10, 2013 the company announced support for "in-stream" payments on Twitter, allowing buyers to purchase items without leaving the Twitter.com stream. Twitter shut down Ribbon's API access after approximately an hour and a half, according to Head of Business Development, Daniel Brusilovsky. Ribbon requested permission to show video cards, but after receiving permission then switched the url to show the hacked checkout system. The company wrote a statement announcing they will revert to showcasing only a summary of their product without the ability to do in-stream payments. As of April 11, 2013 Ribbon links inside Twitter no longer work in-stream and buyers are redirected to purchase on the Ribbon website.
Stream
A stream is a body of water with a current, confined within a bed and stream banks. Depending on its location or certain characteristics, a stream may be referred to as a branch, brook, beck, burn, creek, crick, gill (occasionally ghyll), kill, lick, mill race, rill, river, syke, bayou, rivulet, streamage, wash, run, or runnel.
Streams are important as conduits in the water cycle, instruments in groundwater recharge, and corridors for fish and wildlife migration. The biological habitat in the immediate vicinity of a stream is called a riparian zone. Given the status of the ongoing Holocene extinction, streams play an important corridor role in connecting fragmented habitats and thus in conserving biodiversity. The study of streams and waterways in general is known as surface hydrology and is a core element of environmental geography.
Types
Podcasts:
