Hyperbolic manifold

In mathematics, a hyperbolic manifold is a space where every point looks locally like hyperbolic space of some dimension. They are especially studied in dimensions 2 and 3, where they are called hyperbolic surfaces and hyperbolic 3-manifolds, respectively. In these dimensions, they are important because most manifolds can be made into a hyperbolic manifold by a homeomorphism. This is a consequence of the uniformization theorem for surfaces and the geometrization theorem for 3-manifolds proved by Perelman.

Rigorous Definition

A hyperbolic 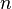-manifold is a complete Riemannian n-manifold of constant sectional curvature -1.

Every complete, connected, simply-connected manifold of constant negative curvature −1 is isometric to the real hyperbolic space . As a result, the universal cover of any closed manifold M of constant negative curvature −1 is . Thus, every such M can be written as where Γ is a torsion-free discrete group of isometries on . That is, Γ is a discrete subgroup of . The manifold has finite volume if and only if Γ is a lattice.

Hyperbolic 3-manifold

A hyperbolic 3-manifold is a 3-manifold equipped with a complete Riemannian metric of constant sectional curvature -1. In other words, it is the quotient of three-dimensional hyperbolic space by a subgroup of hyperbolic isometries acting freely and properly discontinuously. See also Kleinian model.

Its thick-thin decomposition has a thin part consisting of tubular neighborhoods of closed geodesics and/or ends which are the product of a Euclidean surface and the closed half-ray. The manifold is of finite volume if and only if its thick part is compact. In this case, the ends are of the form torus cross the closed half-ray and are called cusps.

Constructions

The first cusped hyperbolic 3-manifold to be discovered was the Gieseking manifold, in 1912. It is constructed by glueing faces of an ideal hyperbolic tetrahedron together.

The complements of knots and links in the 3-sphere are frequently cusped hyperbolic manifolds. Examples include the complements of the figure-eight knot and the Borromean rings and the Whitehead link. More generally, geometrization implies that a knot which is neither a satellite knot nor a torus knot is a hyperbolic knot.