Graded ring

In mathematics, in particular abstract algebra, a graded ring is a ring that is a direct sum of abelian groups such that . The index set is usually the set of nonnegative integers or the set of integers, but can be any monoid or group. The direct sum decomposition is usually referred to as gradation or grading.

A graded module is defined similarly (see below for the precise definition). It generalizes graded vector spaces. A graded module that is also a graded ring is called a graded algebra. A graded ring could also be viewed as a graded Z-algebra.

The associativity is not important (in fact not used at all) in the definition of a graded ring; hence, the notion applies to a non-associative algebra as well; e.g., one can consider a graded Lie algebra.

First properties

Let

be a graded ring.

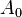is a subring of A (in particular, the additive identity 0 and the multiplicative identity 1 are homogeneous elements of degree zero.)

A commutative -graded ring is a Noetherian ring if and only if is Noetherian and A is finitely generated as an algebra over . For such a ring, the generators may be taken to be homogeneous.