Graded manifold

In algebraic geometry, Graded manifolds are extensions of the manifold concept based on ideas coming from supersymmetry and supercommutative algebra. Both graded manifolds and supermanifolds are phrased in terms of sheaves of graded commutative algebras. However, graded manifolds are characterized by sheaves on smooth manifolds, while supermanifolds are constructed by gluing of sheaves of supervector spaces.

Graded manifolds

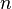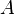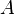A graded manifold of dimension $(n,m)$ is defined as a locally ringed space $(Z,A)$ where $Z$ is an $n$ -dimensional smooth manifold and $A$ is a $C^\infty_Z$ -sheaf of Grassmann algebras of rank $m$ where $C^\infty_Z$ is the sheaf of smooth real functions on $Z$ . The sheaf $A$ is called the structure sheaf of the graded manifold $(Z,A)$ , and the manifold $Z$ is said to be the body of $(Z,A)$ . 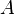Sections of the sheaf $A$ are called graded functions on a graded manifold $(Z,A)$ . They make up a graded commutative $C^\infty(Z)$ -ring $A(Z)$ called the structure ring of $(Z,A)$ . The well-known Batchelor theorem and Serre-Swan theorem characterize graded manifolds as follows.