Function problem

In computational complexity theory, a function problem is a computational problem where a single output (of a total function) is expected for every input, but the output is more complex than that of a decision problem, that is, it isn't just YES or NO.

Formal definition

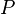A functional problem is defined as a relation over a cartesian product over strings of an arbitrary alphabet :

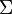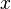An algorithm solves if for every input such that there exists a satisfying , the algorithm produces one such .

Examples

A well-known function problem is given by the Functional Boolean Satisfiability Problem, FSAT for short. The problem, which is closely related to the SAT decision problem can be formulated as follows:

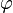Given a boolean formula with variables , find an assignment such that evaluates to or decide that no such assignment exists.

In this case the relation is given by tuples of suitably encoded boolean formulas and satisfying assignments.

Other notable examples include the travelling salesman problem, which asks for the route taken by the salesman, and the integer factorization problem, which asks for the list of factors.