Thermal expansion

Thermal expansion is the tendency of matter to change in shape, area, and volume in response to a change in temperature, through heat transfer.

Temperature is a monotonic function of the average molecular kinetic energy of a substance. When a substance is heated, the kinetic energy of its molecules increases. Thus, the molecules begin moving more and usually maintain a greater average separation. Materials which contract with increasing temperature are unusual; this effect is limited in size, and only occurs within limited temperature ranges (see examples below). The degree of expansion divided by the change in temperature is called the material's coefficient of thermal expansion and generally varies with temperature.

Overview

Predicting expansion

If an equation of state is available, it can be used to predict the values of the thermal expansion at all the required temperatures and pressures, along with many other state functions.

Contraction effects (negative thermal expansion)

Expansive

In mathematics, the notion of expansivity formalizes the notion of points moving away from one another under the action of an iterated function. The idea of expansivity is fairly rigid, as the definition of positive expansivity, below, as well as the Schwarz-Ahlfors-Pick theorem demonstrate.

Definition

If is a metric space, a homeomorphism is said to be expansive if there is a constant

called the expansivity constant, such that for any pair of points in there is an integer 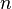such that

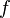Note that in this definition, can be positive or negative, and so may be expansive in the forward or backward directions.

The space is often assumed to be compact, since under that assumption expansivity is a topological property; i.e. if is any other metric generating the same topology as , and if is expansive in , then is expansive in (possibly with a different expansivity constant).

If

is a continuous map, we say that is positively expansive (or forward expansive) if there is a

such that, for any in , there is an such that .