Division (mathematics)
In mathematics, especially in elementary arithmetic, division (denoted ÷ or / or —) is an arithmetic operation. Specifically, if b times c equals a, written:
where b is not zero, then a divided by b equals c, written:
For instance,
since
In the above expressions, a is called the dividend, b is called the divisor, and c is called the quotient; in the expression 
or 
a is also called the numerator and b is also called the denominator.
Conceptually, division of integers can be viewed in either of two distinct but related ways quotition and partition:
Division (horticulture)
Division, in horticulture and gardening, is a method of asexual plant propagation, where the plant (usually an herbaceous perennial) is broken up into two or more parts. Both the root and crown of each part is kept intact. The technique is of ancient origin, and has long been used to propagate bulbs such as garlic and saffron. Division is mainly practiced by gardeners and very small nurseries, as most commercial plant propagation is now done through plant tissue culture.
Division is one of the three main methods used by gardeners to increase stocks of plants (the other two are seed-sowing and cuttings). Division is usually applied to mature perennial plants, but may also be used for shrubs with suckering roots, such as gaultheria, kerria and sarcococca. Annual and biennial plants do not lend themselves to this procedure, as their lifespan is too short.
Most perennials are best divided and replanted every few years to keep them healthy. They may also be divided in order to produce new plants. Those with woody crowns or fleshy roots need to be cut apart, while others can be prized apart using garden forks or hand forks. Each separate section must have both shoots and roots. Division can take place at almost any time of the year, but the best seasons are Autumn and Spring.
Division of the field
In heraldry, the field (background) of a shield can be divided into more than one area, or subdivision, of different tinctures, usually following the lines of one of the ordinaries and carrying its name (e.g. a shield divided in the shape of a chevron is said to be parted "per chevron"). Shields may be divided this way for differencing (to avoid conflict with otherwise similar coats of arms) or for purposes of marshalling (combining two or more coats of arms into one), or simply for style. The lines that divide a shield may not always be straight, and there is a system of terminology for describing patterned lines, which is also shared with the heraldic ordinaries. French heraldry takes a different approach in many cases from the one described in this article.
Common divisions of the field
Common partitions of the field are:
Division algorithm
A division algorithm is an algorithm which, given two integers N and D, computes their quotient and/or remainder, the result of division. Some are applied by hand, while others are employed by digital circuit designs and software.
Division algorithms fall into two main categories: slow division and fast division. Slow division algorithms produce one digit of the final quotient per iteration. Examples of slow division include restoring, non-performing restoring, non-restoring, and SRT division. Fast division methods start with a close approximation to the final quotient and produce twice as many digits of the final quotient on each iteration. Newton–Raphson and Goldschmidt fall into this category.
Discussion will refer to the form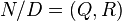 
, where
is the input, and
is the output.
Division by repeated subtraction
The simplest division algorithm, historically incorporated into a greatest common divisor algorithm presented in Euclid's Elements, Book VII, Proposition 1, finds the remainder given two positive integers using only subtractions and comparisons:
Podcasts:
