Current

Current may refer to:

Ongoing events

Science and mathematics

Arts and entertainment

Other uses

See also

Current (album)

Current is the fifth album by funk-disco band Heatwave, released in 1982 on the Epic label. It was produced by Barry Blue.

Track listing

All songs written and composed by Rod Temperton, except where noted. 

Personnel

Charts

Singles

References

External links

Current (mathematics)

In mathematics, more particularly in functional analysis, differential topology, and geometric measure theory, a k-current in the sense of Georges de Rham is a functional on the space of compactly supported differential k-forms, on a smooth manifold M. Formally currents behave like Schwartz distributions on a space of differential forms. In a geometric setting, they can represent integration over a submanifold, generalizing the Dirac delta function, or more generally even directional derivatives of delta functions (multipoles) spread out along subsets of M.

Definition

Let denote the space of smooth m-forms with compact support on a smooth manifold . A current is a linear functional on which is continuous in the sense of distributions. Thus a linear functional

is an m-current if it is continuous in the following sense: If a sequence of smooth forms, all supported in the same compact set, is such that all derivatives of all their coefficients tend uniformly to 0 when 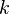tends to infinity, then tends to 0.

Dial

Dial may refer to:

Mechanical device

DIAL

Other

Dial (band)

Dial is a progressive rock band based in the Netherlands.

History

Dial was founded in late 2003 by Liselotte Hegt, Rommert van der Meer and Kristoffer Gildenlöw. Early on, the band was pure a hobby but after Kristoffer's departure from Swedish prog metal band Pain of Salvation in early 2006, the band headed towards a more serious destiny.

In summer 2006, the band went to Austria to record their debut album Synchronized together with producer Devon Graves (of Deadsoul Tribe and Psychotic Waltz). This album was released in May 2007 through Prog Rock Records (US).

Line-up

External links

Rotary dial

A rotary dial is a component of a telephone or a telephone switchboard that implements a signaling technology in telecommunications known as pulse dialing. It is used when initiating a telephone call to transmit the destination telephone number to a telephone exchange.

On the rotary dial, the digits are arranged in a circular layout so that a finger wheel may be rotated with one finger from the position of each digit to a fixed stop position, implemented by the finger stop, which is a mechanical barrier to prevent further rotation. When released at the finger stop, the wheel returns to its home position by spring action at a speed regulated by a governor device. During this return rotation, the dial interrupts the direct electrical current of the telephone line (local loop) a specific number of times for each digit and thereby generates electrical pulses which the telephone exchange decodes into each dialed digit. Each of the ten digits are encoded in sequences of up to ten pulses. For this reason, the method is sometimes called decadic dialling.