Density matrix
A density matrix is a matrix that describes a quantum system in a mixed state, a statistical ensemble of several quantum states. This should be contrasted with a single state vector that describes a quantum system in a pure state. The density matrix is the quantum-mechanical analogue to a phase-space probability measure (probability distribution of position and momentum) in classical statistical mechanics.
Explicitly, suppose a quantum system may be found in state 
with probability p1, or it may be found in state 
with probability p2, or it may be found in state 
with probability p3, and so on. The density operator for this system is
where 
need not be orthogonal and 
. By choosing an orthonormal basis 
, one may resolve the density operator into the density matrix, whose elements are
The density operator can also be defined in terms of the density matrix,
For an operator 
(which describes an observable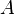 
of the system), the expectation value 
is given by
In words, the expectation value of A for the mixed state is the sum of the expectation values of A for each of the pure states 
weighted by the probabilities pi and can be computed as the trace of the product of the density matrix with the matrix representation of 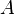in the same basis.
