Latest News for: density function
Edit
U.S. Bone & Joint Health Supplements Market to Reach $4.11 Billion by 2029, Driven by ...
GetNews 28 Mar 2025
Edit
Dynamic density functional theory offers new approach to understanding protein–membrane interactions
Phys Dot Org 25 Mar 2025
....
Edit
The Ozempic workout? How gyms and trainers are catering to a new group of exercisers
Detroit news 25 Mar 2025
Edit
Physical fitness: science, health and quality of life
CyprusMail 21 Mar 2025
Fitness is not just about how fast we run or how much weight we lift but about how efficiently our body functions in daily life ... Strength training helps increase muscle mass and bone density, decreasing the likelihood of osteoporosis.
Edit
Korean scientists tackle explosive batteries, promise 620-mile range for future EVs
Interesting Engineering 20 Mar 2025
Edit
What is Baby Feet? Know all about the condition that might bar Sunita Williams from walking after her return to Earth
The Times of India 20 Mar 2025
Edit
Nasa Astronaut Sunita Williams Begins 45-Day Rehabilitation Programme To Tackle Likely Health Challenges After Prolonged ...
Zeenews 19 Mar 2025
Edit
Swollen eyeballs, baby-like skin, and gravity shock: What Sunita Williams and Butch Wilmore might experience upon returning to Earth
The Times of India 17 Mar 2025
Edit
Doctor reveals six hugely popular supplements that might be causing silent health crises in your ...
The Daily Mail 16 Mar 2025
Magnesium is essential for maintaining bone density, muscle function, and heart health.
Edit
Airbnb restrictions in Louisville at risk under revised Kentucky bill
Courier Journal 14 Mar 2025
Discover key facts about the Kentucky General Assembly, including its history, structure, and state government functions ... "This is functionally allowing, without restriction, commercial operations in residential zones," Winkler said.
Edit
Take 'precautionary approach' on deep-sea mining: top official tells AFP
Raw Story 14 Mar 2025
by Sara HUSSEIN ... ALSO READ. 'The Hard Reset' ... And while scientists are still learning about life on the seafloor, deep-sea ecosystems "tend to have lower population densities and function under vastly different environmental conditions," Carvalho said ... .
Edit
Why we need more female astronauts to understand spaceflight health
Interesting Engineering 14 Mar 2025- 1
- 2
- Next page »


 , if a
, if a 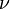 on
on  , such that for any measurable subset
, such that for any measurable subset  ,
, .
.