A definition (≝) is a passage that explains the meaning of a term (a word, phrase or other set of symbols), or a type of thing. The term to be defined is the definiendum. A term may have many different senses or meanings. For each such specific sense, a definiens is a cluster of words that defines that term.
A chief difficulty in managing definition is the need to use other terms that are already understood or whose definitions are easily obtainable. The use of the term in a simple example may suffice. By contrast, a dictionary definition has additional details, typically including an etymology showing snapshots of the earlier meanings and the parent language.
Like other words, the term definition has subtly different meanings in different contexts. A definition may be descriptive of the general use meaning, or stipulative of the speaker's immediate intentional meaning. For example, in formal languages like mathematics, a 'stipulative' definition guides a specific discussion. A descriptive definition can be shown to be "right" or "wrong" by comparison to general usage, but a stipulative definition can only be disproved by showing a logical contradiction.[1]
A precising definition extends the descriptive dictionary definition (lexical definition) of a term for a specific purpose by including additional criteria that narrow down the set of things meeting the definition.
C.L. Stevenson has identified persuasive definition as a form of stipulative definition which purports to describe the "true" or "commonly accepted" meaning of a term, while in reality stipulating an altered use, perhaps as an argument for some specific view.
Stevenson has also noted that some definitions are "legal" or "coercive", whose object is to create or alter rights, duties or crimes.[2]
Contents |
Intension and extension [link]
An intensional definition, also called a coactive definition, specifies the necessary and sufficient conditions for a thing being a member of a specific set. Any definition that attempts to set out the essence of something, such as that by genus and differentia, is an intensional definition.
An extensional definition, also called a denotative definition, of a concept or term specifies its extension. It is a list naming every object that is a member of a specific set.
So, for example, an intensional definition of 'Prime Minister' might be the most senior minister of a cabinet in the executive branch of government in a parliamentary system. An extensional definition would be a list of all past, present and future prime ministers.
One important form of the extensional definition is ostensive definition. This gives the meaning of a term by pointing, in the case of an individual, to the thing itself, or in the case of a class, to examples of the right kind. So you can explain who Alice (an individual) is by pointing her out to me; or what a rabbit (a class) is by pointing at several and expecting me to 'catch on'. The process of ostensive definition itself was critically appraised by Ludwig Wittgenstein.[3]
An enumerative definition of a concept or term is an extensional definition that gives an explicit and exhaustive listing of all the objects that fall under the concept or term in question. Enumerative definitions are only possible for finite sets and only practical for relatively small sets.[citation needed]
[edit] Divisio and partitio
Divisio and partitio are classical terms for definitions. A partitio is simply an intensional definition. A divisio is not an extensional definition. Divisio is an exhaustive list of subsets of a set, in the sense that every member of the "divided" set is a member of one of the subsets. An extreme form of divisio lists all sets whose only member is a member of the "divided" set. The difference between this and an extensional definition is that extensional definitions list members, and not sets.[4]
Definition by genus and differentia [link]
A genus–differentia definition is a type of intensional definition, and it is composed by two parts:
- a genus (or family): An existing definition that serves as a portion of the new definition; all definitions with the same genus are considered members of that genus.
- the differentia: The portion of the new definition that is not provided by the genera.
For example, consider these two definitions:
- a triangle: A plane figure that has 3 straight bounding sides.
- a quadrilateral: A plane figure that has 4 straight bounding sides.
Those definitions can be expressed as a genus and 2 differentiae:
- a genus: A plane figure.
- 2 differentiae:
- the differentia for a triangle: that has 3 straight bounding sides.
- the differentia for a quadrilateral: that has 4 straight bounding sides.
When multiple definitions could serve equally well, then all such definitions apply simultaneously. For instance, given the following:
- a rectangle: a quadrilateral that has interior angles which are all right angles.
- a rhombus: a quadrilateral that has bounding sides which all have the same length.
both of these definitions of 'square' are equally acceptable:
- a square: a rectangle that is a rhombus.
- a square: a rhombus that is a rectangle.
Thus, a 'square' is a member of both the genus 'rectangle' and the genus 'rhombus'. In such a case, it is notationally convenient to consolidate the definitions into one definition that is expressed with multiple genera (and possibly no differentia, as in the following):
- a square: a rectangle and a rhombus.
or completely equivalently:
- a square: a rhombus and a rectangle.
Rules for definition by genus and differentia [link]
Certain rules have traditionally been given for this particular type of definition.[5][6][7]
- A definition must set out the essential attributes of the thing defined.
- Definitions should avoid circularity. To define a horse as 'a member of the species equus' would convey no information whatsoever. For this reason, Locking[specify] adds that a definition of a term must not comprise of terms which are synonymous with it. This would be a circular definition, a circulus in definiendo. Note, however, that it is acceptable to define two relative terms in respect of each other. Clearly, we cannot define 'antecedent' without using the term 'consequent', nor conversely.
- The definition must not be too wide or too narrow. It must be applicable to everything to which the defined term applies (i.e. not miss anything out), and to nothing else (i.e. not include any things to which the defined term would not truly apply).
- The definition must not be obscure. The purpose of a definition is to explain the meaning of a term which may be obscure or difficult, by the use of terms that are commonly understood and whose meaning is clear. The violation of this rule is known by the Latin term obscurum per obscurius. However, sometimes scientific and philosophical terms are difficult to define without obscurity. (See the definition of Free will in Wikipedia, for instance).
- A definition should not be negative where it can be positive. We should not define 'wisdom' as the absence of folly, or a healthy thing as whatever is not sick. Sometimes this is unavoidable, however. We cannot define a point except as 'something with no parts', nor blindness except as 'the absence of sight in a creature that is normally sighted'.
Essence [link]
In classical thought, a definition was taken to be a statement of the essence of a thing. Aristotle had it that an object's essential attributes form its "essential nature", and that a definition of the object must include these essential attributes.[8]
The idea that a definition should state the essence of a thing led to the distinction between nominal and real essence, originating with Aristotle. In a passage from the Posterior Analytics,[9] he says that we can know the meaning of a made-up name (he gives the example 'goat stag'), without knowing what he calls the 'essential nature' of the thing that the name would denote, if there were such a thing. This led medieval logicians to distinguish between what they called the quid nominis or 'whatness of the name', and the underlying nature common to all the things it names, which they called the quid rei or 'whatness of the thing'. (Early modern philosophers like Locke used the corresponding English terms 'nominal essence' and 'real essence'). The name 'hobbit', for example, is perfectly meaningful. It has a quid nominis. But we could not know the real nature of hobbits, even if there were such things, and so we cannot know the real nature or quid rei of hobbits. By contrast, the name 'man' denotes real things (men) that have a certain quid rei. The meaning of a name is distinct from the nature that thing must have in order that the name apply to it.
This leads to a corresponding distinction between nominal and real definition. A nominal definition is the definition explaining what a word means, i.e. which says what the 'nominal essence' is, and is definition in the classical sense as given above. A real definition, by contrast, is one expressing the real nature or quid rei of the thing.
This preoccupation with essence dissipated in much of modern philosophy. Analytic philosophy in particular is critical of attempts to elucidate the essence of a thing. Russell described it as "a hopelessly muddle-headed notion".[10]
More recently Kripke's formalisation of possible world semantics in modal logic led to a new approach to essentialism. Insofar as the essential properties of a thing are necessary to it, they are those things it possesses in all possible worlds. Kripke refers to names used in this way as rigid designators.
Recursive definitions [link]
A recursive definition, sometimes also called an inductive definition, is one that defines a word in terms of itself, so to speak, albeit in a useful way. Normally this consists of three steps:
- At least one thing is stated to be a member of the set being defined; this is sometimes called a "base set".
- All things bearing a certain relation to other members of the set are also to count as members of the set. It is this step that makes the definition recursive.
- All other things are excluded from the set
For instance, we could define natural number as follows (after Peano):
- "0" is a natural number.
- Each natural number has a distinct successor, such that:
- the successor of a natural number is also a natural number, and
- no natural number is succeeded by "0".
- Nothing else is a natural number.
So "0" will have exactly one successor, which for convenience we can call "1". In turn, "1" will have exactly one successor, which we would call "2", and so on. Notice that the second condition in the definition itself refers to natural numbers, and hence involves self-reference. Although this sort of definition involves a form of circularity, it is not vicious, and the definition has been quite successful.
Working definitions [link]
A working definition is either chosen for an occasion and may not fully conform with established or authoritative definitions. Not knowing of established definitions would be grounds for selecting or devising a working definition. Or it refers to a definition being developed; a tentative definition that can be tailored to create an authoritative definition.
Limitations of definition [link]
Given that a natural language such as English contains, at any given time, a finite number of words, any comprehensive list of definitions must either be circular or rely upon primitive notions. If every term of every definiens must itself be defined, "where at last should we stop?"[11][12] A dictionary, for instance, insofar as it is a comprehensive list of lexical definitions, must resort to circularity.[13][14][15]
Many philosophers have chosen instead to leave some terms undefined. The scholastic philosophers claimed that the highest genera (the so-called ten generalissima) cannot be defined, since we cannot assign any higher genus under which they may fall. Thus we cannot define being, unity and similar concepts.[6] Locke supposes in An Essay Concerning Human Understanding[16] that the names of simple concepts do not admit of any definition. More recently Bertrand Russell sought to develop a formal language based on logical atoms. Other philosophers, notably Wittgenstein, rejected the need for any undefined simples. Wittgenstein pointed out in his Philosophical Investigations that what counts as a "simple" in one circumstance might not do so in another.[17] He rejected the very idea that every explanation of the meaning of a term needed itself to be explained: "As though an explanation hung in the air unless supported by another one",[18] claiming instead that explanation of a term is only needed when we need to avoid misunderstanding.
Locke and Mill also argued that we cannot define individuals. We learn names by connecting an idea with a sound, so that speaker and hearer have the same idea when the same word is used.[19] This is not possible when no one else is acquainted with the particular thing that has "fallen under our notice".[20] Russell offered his theory of descriptions in part as a way of defining a proper name, the definition being given by a definite description that "picks out" exactly one individual. Saul Kripke pointed to difficulties with this approach, especially in relation to modality, in his book Naming and Necessity.
There is a presumption in the classic example of a definition that the definiens can be stated. Wittgenstein argued that for some terms this is not the case.[21] The examples he used include game, number and family. In such cases, he argued, there is no fixed boundary that can be used to provide a definition. Rather, the items are grouped together because of a family resemblance. For terms such as these it is not possible and indeed not necessary to state a definition; rather, one simply comes to understand the use of the term.
In medicine [link]
In medical dictionaries, definitions should to the greatest extent possible be:
- simple and easy to understand,[22] preferably even by the general public;[23]
- useful clinically[23] or in related areas where the definition will be used;[22]
- specific,[22] that is, by reading the definition only, it should ideally not be possible to refer to any other entity than the definiendum;
- measurable;[22]
- reflecting current scientific knowledge.[22][23]
See also [link]
- Analytic proposition
- Definable set
- Definitionism
- Ostensive definition
- Demonstration
- Extensional definition
- Fallacies of definition
- Circular definition
- Indeterminacy
- Intensional definition
- Lexical definition
- Ramsey–Lewis method
- Semantic
- Synthetic proposition
- Theoretical definition
Notes [link]
- ^ https://www.sfu.ca/philosophy/swartz/definitions.htm#part5.1
- ^ Stevenson, C.L., Ethics and Language, Connecticut 1944
- ^ Philosophical investigations, Part 1 §27-34
- ^ Katerina Ierodiakonou, "The Stoic Division of Philosophy", in Phronesis: A Journal for Ancient Philosophy, Volume 38, Number 1, 1993 , pp. 57-74.
- ^ Copi 1982 pp 165-169
- ^ a b Joyce, Ch. X
- ^ Joseph, Ch. V
- ^ Posterior Analytics, Bk 1 c. 4
- ^ Posterior Analytics Bk 2 c. 7
- ^ A history of Western Philosophy, p. 210
- ^ Locke, Essay, Bk. III, Ch. iv, 5
- ^ This problem parallels the diallelus, but leads to scepticism about meaning rather than knowledge.
- ^ Generally lexicographers seek to avoid circularity wherever possible, but the definitions of words such as "the" and "a" use those words and are therefore circular. [1] [2] Lexicographer Sidney I. Landau's essay "Sexual Intercourse in American College Dictionaries" provides other examples of circularity in dictionary definitions. (McKean, p. 73-77)
- ^ An exercise suggested by J. L. Austin involved taking up a dictionary and finding a selection of terms relating to the key concept, then looking up each of the words in the explanation of their meaning. Then, iterating this process until the list of words begins to repeat, closing in a “family circle” of words relating to the key concept.
(A plea for excuses in Philosophical Papers. Ed. J. O. Urmson and G. J. Warnock. Oxford: Oxford UP, 1961. 1979.) - ^ In the game of Vish, players compete to find circularity in a dictionary.
- ^ Locke, Essay, Bk. III, Ch. iv
- ^ See especially Philosophical Investigations Part 1 §48
- ^ He continues: "Whereas an explanation may indeed rest on another one that has been given, but none stands in need of another - unless we require it to prevent a misunderstanding. One might say: an explanation serves to remove or to avert a misunderstanding - one, that is, that would occur but for the explanation; not every one I can imagine." Philosophical Investigations, Part 1 §87, italics in original
- ^ This theory of meaning is one of the targets of the private language argument
- ^ Locke, Essay, Bk. III, Ch. iii, 3
- ^ Philosophical Investigations
- ^ a b c d e McPherson, M.; Arango, P.; Fox, H.; Lauver, C.; McManus, M.; Newacheck, P.; Perrin, J.; Shonkoff, J. et al. (1998). "A new definition of children with special health care needs". Pediatrics 102 (1 Pt 1): 137–140. DOI:10.1542/peds.102.1.137. PMID 9714637.
- ^ a b c Morse, R. M.; Flavin, D. K. (1992). "The Definition of Alcoholism". JAMA 268 (8): 1012–1014. DOI:10.1001/jama.1992.03490080086030. PMID 1501306.
References [link]
- Copi, Irving (1982). Introduction to Logic. New York: Macmillan. ISBN 0-02-977520-5.
- Joseph, Horace William Brindley (1916 repr. 2000). An Introduction to Logic, 2nd edition. Clarendon Press repr. Paper Tiger. ISBN 1-889439-17-7. (full text of 1st ed. (1906))
- Joyce, George Hayward (1926). Principles of logic, 3d ed., new impression. London, New York: Longmans, Green and co. (worldcat) (full text of 2nd ed. (1916))
- Locke, John (1690). An Essay Concerning Human Understanding. ISBN 0-14-043482-8. (full text: vol 1, vol 2)
- McKean, Erin (2001). Verbatim: From the bawdy to the sublime, the best writing on language for word lovers, grammar mavens, and armchair linguists. Harvest Books. ISBN 0-15-601209-X.
- Robinson, Richard (1954). Definition. Oxford: At The Clarendon Press. ISBN 978-0-19-824160-7. https://books.google.com/?id=WVt8TfDR-YAC&lpg=PP1&dq=richard%20robinson%20definition&pg=PP1#v=onepage&q.
- Simpson, John; Edmund Weiner (1989). Oxford English Dictionary, second edition (20 volumes). Oxford University Press. ISBN 0-19-861186-2.
- Wittgenstein, Ludwig (1953/2001). Philosophical Investigations. Blackwell Publishing. ISBN 0-631-23127-7.
External links [link]
| Look up definition in Wiktionary, the free dictionary. |
- Definitions at Synonyms.Me
- Definitions, Stanford Encyclopedia of Philosophy Gupta, Anil (2008)
- Definitions, Dictionaries, and Meanings, Norman Swartz 1997
- Guy Longworth (ca. 2008) "Definitions: Uses and Varieties of". = in: K. Brown (ed.): Elsevier Encyclopedia of Language and Linguistics, Elsevier.
- Definition and Meaning, a very short introduction by Garth Kemerling (2001).
https://wn.com/Definition

(ε, δ)-definition of limit
In calculus, the (ε, δ)-definition of limit ("epsilon-delta definition of limit") is a formalization of the notion of limit. It was first given by Bernard Bolzano in 1817. Augustin-Louis Cauchy never gave an (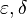 ) definition of limit in his Cours d'Analyse, but occasionally used
) definition of limit in his Cours d'Analyse, but occasionally used 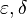 arguments in proofs. The definitive modern statement was ultimately provided by Karl Weierstrass.
arguments in proofs. The definitive modern statement was ultimately provided by Karl Weierstrass.
History
Isaac Newton was aware, in the context of the derivative concept, that the limit of the ratio of evanescent quantities was not itself a ratio, as when he wrote:
Occasionally Newton explained limits in terms similar to the epsilon-delta definition.Augustin-Louis Cauchy gave a definition of limit in terms of a more primitive notion he called a variable quantity. He never gave an epsilon-delta definition of limit (Grabiner 1981). Some of Cauchy's proofs contain indications of the epsilon-delta method. Whether or not his foundational approach can be considered a harbinger of Weierstrass's is a subject of scholarly dispute. Grabiner feels that it is, while Schubring (2005) disagrees. Nakane concludes that Cauchy and Weierstrass gave the same name to different notions of limit.

Definition (album)
Definition is the sixth album by the American crossover thrash band D.R.I., which was released in 1992.
Track listing
Bonus tracks
LP - "Out of Mind"
Cassette - "Hide Your Eyes"
CD - "Dry Heaves"
Credits
Atmosphere (unit)
The standard atmosphere (symbol: atm) is a unit of pressure defined as 101325 Pa (1.01325 bar). It is sometimes used as a reference or standard pressure.
History
In 1954 the 10th Conférence Générale des Poids et Mesures (CGPM) adopted standard atmosphere for general use and affirmed its definition of being precisely equal to 1,013,250 dynes per square centimetre (101325 Pa). This value was intended to represent the mean atmospheric pressure at mean sea level at the latitude of Paris, France, and does reflect the mean sea level pressure for many industrialized nations that are at broadly similar latitudes.
In chemistry and in various industries, the reference pressure referred to in “Standard Temperature and Pressure” (STP) was commonly 1 atm (101.325 kPa) but standards have since diverged; in 1982, the International Union of Pure and Applied Chemistry (IUPAC) recommended that for the purposes of specifying the physical properties of substances, “standard pressure” should be precisely 100 kPa (1 bar).
Atmosphere (journal)
Atmosphere is a monthly peer-reviewed open access scientific journal covering research related to the Earth`s atmosphere. The journal is published by MDPI and was established in 2010. The founding editor-in-chief was Daniela Jacob (Max-Planck-Institute for Meteorology) until 2014. The current editor-in-chief is Robert Talbot (University of Houston).
Abstracting and indexing
Atmosphere is covered by the following indexing and abstracting databases:
According to the Journal Citation Reports, the journal has a 2014 impact factor of 1.132.
Features of Atmosphere

Atmosphere (Kaskade album)
Atmosphere is the eighth studio album of American house DJ and electronic dance music producer Kaskade. It was released in the United States and Canada on September 10, 2013 through Ultra Records.
Reception
The album shares similar success with his previous studio album Fire & Ice. It became Kaskade's second No. 1 on the Billboard Dance/Electronic Albums chart. It also made its debut at #16 on the Billboard Top 200 chart, as well as number 7 on the Billboard Digital Albums chart and number 2 on the Billboard Independent Albums chart. Atmosphere earned Kaskade his second Grammy nomination for Best Dance/Electronica Album in 2014.
The album received mixed reviews from mainstream critics. Metacritic rated Atmosphere an average score of 62 out of 100 based on 5 reviews.
Track listing
All songs written and composed by Ryan Raddon and Finn Bjarnson, except for tracks 3, 7 and 11.
Credits and personnel
Credits adapted from AllMusic and Discogs.
Chart performance
Release history
Tight
Tight may refer to:


